Infinities of Increasing Order

Sequences that diverge to infinity as n→∞ can be compared using the Ratio Test for sequences. Such sequences are referred to as infinities of increasing order.

What is an infinity of increasing order?

An infinity of increasing order grows unboundedly faster than other divergent sequences used as a benchmark for comparison.

A Practical Example

Let’s consider the following two sequences for k > 0:

$$ n^k $$

$$ k^n $$

Both sequences have strictly positive terms and diverge to infinity as n→∞:

$$ \lim_{ n \rightarrow ∞} n^k = ∞ $$

$$ \lim_{ n \rightarrow ∞} k^n = ∞ $$

But which one grows faster as n increases?

To answer this, we define a new sequence a_n as the ratio of the two sequences:

$$ a_n = \frac{ n^k }{ k^n } $$

Next, we define a sequence b_n as the ratio between consecutive terms of a_n:

$$ b_n = \frac{a_{n+1}}{a_n} $$

$$ b_n = \frac{ \frac{ (n+1)^k }{ k^{(n+1)} } }{ \frac{ n^k }{ k^n } } $$

$$ b_n = \frac{ (n+1)^k }{ k^{n+1} } \cdot \frac{ k^n }{ n^k } $$

$$ b_n = \frac{ (n+1)^k }{ k \cdot n^k } $$

$$ b_n = \frac{1}{k} \cdot \frac{ (n+1)^k }{ n^k } $$

$$ b_n = \frac{1}{k} \cdot \left( \frac{ n+1 }{ n } \right)^k $$

Let’s evaluate the limit of b_n as n→∞:

$$ \lim_{ n \rightarrow ∞} b_n $$

$$ \lim_{ n \rightarrow ∞} \frac{1}{k} \cdot \left( \frac{ n+1 }{ n } \right)^k $$

Since (n+1)/n tends to 1 as n grows without bound, we obtain:

$$ \lim_{ n \rightarrow ∞} \frac{1}{k} \cdot \left( \frac{ n+1 }{ n } \right)^k = \frac{1}{k} < 1 $$

Because the limit of b_n is less than 1, by the Ratio Test for sequences, the sequence a_n converges to zero.

$$ \lim_{ n \rightarrow ∞} a_n = \lim_{ n \rightarrow ∞} \frac{ n^k }{ k^n } = 0 $$

This means the denominator sequence kⁿ is an infinity of higher order relative to n^k.

The graph below clearly illustrates this relationship between the two sequences.

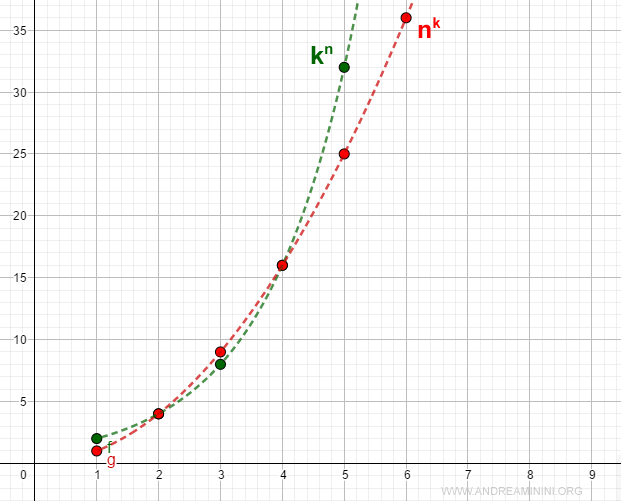
The sequence kⁿ grows towards infinity significantly faster than the sequence n^k.

And so on.