Bolzano-Weierstrass Theorem

Every bounded sequence a_n contains at least one convergent subsequence.

Proof

If a sequence is bounded, then there exist real numbers a and b such that:

$$ a \le a_n \le b $$

Here, a and b represent the lower and upper bounds of the sequence, respectively (or vice versa).

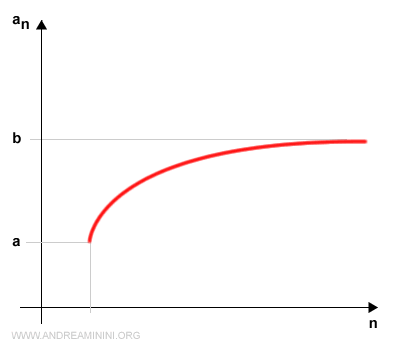
These bounds define a closed interval containing all terms a_n of the sequence along the vertical axis (y-axis).

On the horizontal axis (x-axis), we plot the index n of the sequence.

Note. A sequence a_n consists of infinitely many terms because its index n ranges over the natural numbers, which form an infinite set.

We divide the interval [a, b] into two equal parts by identifying the midpoint c = (a + b)/2.

We thus obtain two subintervals: [a, c] and [c, b].

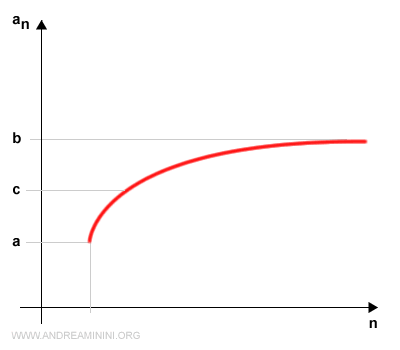
Exactly one of these two subintervals must contain infinitely many terms of the sequence; the other can contain at most finitely many.

By hypothesis, suppose the interval [c, b] contains infinitely many terms of the sequence.

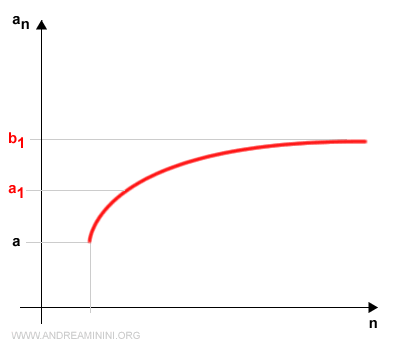
We then relabel this interval as [a₁, b₁]:

$$ [c, b] = [a_1, b_1] $$

No matter which interval we choose, the following inequalities hold:

$$ a \le a_1 $$ $$ b_1 \le b $$

and the length of this new interval is exactly half that of the preceding one:

$$ b_1 - a_1 = \frac{b - a}{2} $$

Let n₁ denote the smallest index of the sequence a_n lying in [a₁, b₁].

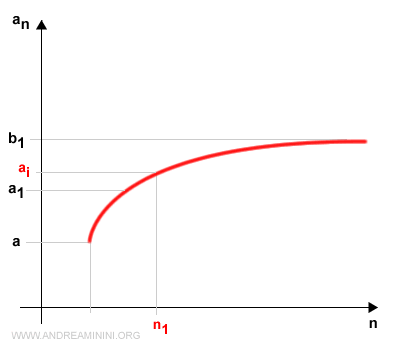
We now subdivide [a₁, b₁] into two subintervals: [a₁, c₁] and [c₁, b₁].

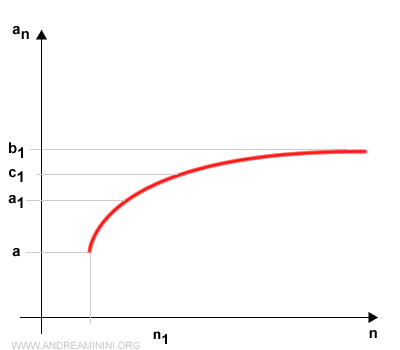
Again, exactly one of these subintervals will contain infinitely many terms of the sequence.

By hypothesis, let [c₁, b₁] be that subinterval containing infinitely many terms.

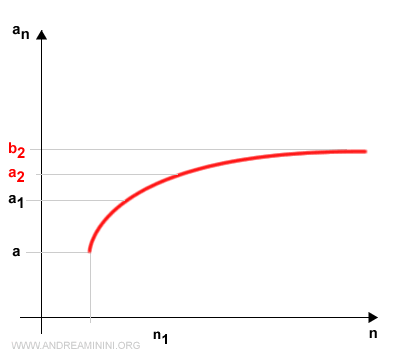
We relabel this interval as [a₂, b₂]:

$$ [c_1, b_1] = [a_2, b_2] $$

Again, we have:

$$ a_1 \le a_2 $$ $$ b_2 \le b_1 $$

and the length of this interval is half that of the previous one:

$$ b_2 - a_2 = \frac{b_1 - a_1}{2} = \frac{b - a}{4} $$

Let n₂ denote the smallest index of the sequence a_n contained in [a₂, b₂].

By construction, n₂ is an integer greater than n₁.

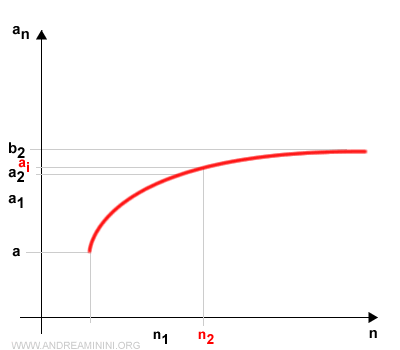
We continue this process iteratively for k steps.

After k iterations, we obtain the chain of inequalities:

$$ a \le a_k \le b_k \le b $$

The length of the interval [a_k, b_k] is:

$$ b_k - a_k = \frac{b - a}{2^k} $$

Let n_k denote the smallest index of a_n in the interval [a_k, b_k].

Each index n_k is strictly greater than the preceding one, n_k-1.

Thus, we construct a sequence of indices:

$$ n_1, n_2, \dots, n_{k-1}, n_k $$

Since these are indices of a_n, all n_k are natural numbers.

Moreover, these indices satisfy:

$$ n_1 < n_2 < \dots < n_{k-1} < n_k $$

Associated with these indices is a subsequence of a_n:

$$ a_{n_1}, a_{n_2}, \dots, a_{n_k} $$

Each term of this subsequence a_nk lies within the interval [a_k, b_k]:

$$ a_{n_k} \in [a_k, b_k] $$

Therefore:

$$ a_k \le a_{n_k} \le b_k $$

From this procedure, we identify three sequences:

• The sequence of lower bounds a_k (the left endpoints of the intervals [a_k, b_k])
• The sequence of first terms a_nk within each interval [a_k, b_k]
• The sequence of upper bounds b_k (the right endpoints of the intervals [a_k, b_k])

The sequences a_k and b_k are monotonic and bounded and each consists of k terms, since:

$$ a \le a_k \le b_k \le b $$

That is:

$$ a \le a_1 \le a_2 \le \dots \le a_k \le b_1 \le b_2 \le \dots \le b_k \le b $$

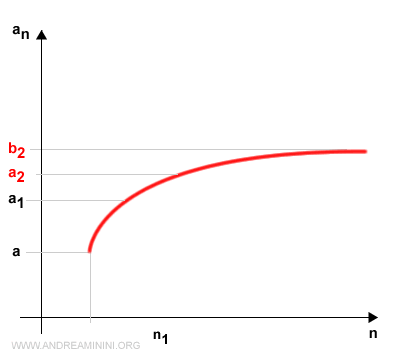
Taking the limits of these sequences as k → ∞, we have:

$$ \lim_{k \rightarrow \infty;} a_k \le \lim_{k \rightarrow \infty;} a_{n_k} \le \lim_{k \rightarrow \infty;} b_k $$

Because a_k and b_k are monotonic and bounded, by the Monotone Convergence Theorem, they both converge to finite limits:

$$ l_1 \le \lim_{k \rightarrow \infty;} a_{n_k} \le l_2 $$

In this construction, the two limits l₁ and l₂ are actually equal (i.e., l₁ = l₂):

$$ l \le \lim_{k \rightarrow \infty;} a_{n_k} \le l $$

Explanation. Since: $$ b_k - a_k = \frac{b - a}{2^k} $$ we have: $$ b_k = a_k + \frac{b - a}{2^k} $$ Hence, the limit of the sequence b_k as k → ∞ equals the limit of a_k: $$ l_2 = \lim_{k \rightarrow \infty;} b_k = \lim_{k \rightarrow \infty;} \left(a_k + \frac{b - a}{2^k}\right) = \lim_{k \rightarrow \infty;} a_k + \lim_{k \rightarrow \infty;} \frac{b - a}{2^k} = \lim_{k \rightarrow \infty;} a_k + 0 = l_1 $$ because the term (b - a)/2^k tends to zero as k → ∞.

By the Squeeze Theorem, the subsequence a_nk also converges to this same finite limit l:

$$ \lim_{k \rightarrow \infty;} a_{n_k} = l $$

Therefore, the subsequence a_nk is convergent.

This concludes the proof of the Bolzano-Weierstrass Theorem.

And so on.