Ratio Test for Sequences

Consider a sequence a_n with positive terms. If the sequence defined by b_n = a_n+1/a_n converges to a limit l_b where l_b < 1, then a_n converges to zero.

A Practical Example

Example 1

Take, for instance, the sequence

$$ a_n = \frac{n^2+1}{2^n} $$

This sequence has positive terms for all n > 0.

Let’s define its ratio sequence, b_n:

$$ b_n = \frac{a_{n+1}}{a_n} = \frac{ \frac{(n+1)^2+1}{2^{n+1}} } { \frac{n^2+1}{2^n} } = \frac{(n+1)^2+1}{2^{n+1}} \cdot \frac{2^n}{n^2+1} $$

$$ b_n = \frac{n^2+2n+1}{2 \cdot 2^n} \cdot \frac{2^n}{n^2+1 }= \frac{n^2+2n+1}{2n^2+2 } $$

As n approaches infinity, the sequence b_n converges to 1/2, which is less than 1. This result comes from the fact that we’re dealing with a rational function where the numerator and denominator are polynomials of the same degree.

So, when computing the limit, we only keep the leading terms, yielding n²/2n² = 1/2.

$$ \lim_{ n \rightarrow ∞} b_n = \lim_{ n \rightarrow ∞} \frac{n^2+2n+1}{2n^2+2 } =\lim_{ n \rightarrow ∞} \frac{n^2}{2n^2} = \frac{1}{2} < 1 $$

Therefore, by the Ratio Test, the sequence a_n converges to zero as n approaches infinity. In other words, a_n is an infinitesimal sequence.

$$ \lim_{ n \rightarrow ∞ } a_n = \lim_{ n \rightarrow ∞ } \frac{n^2+1}{2^n} = 0 $$

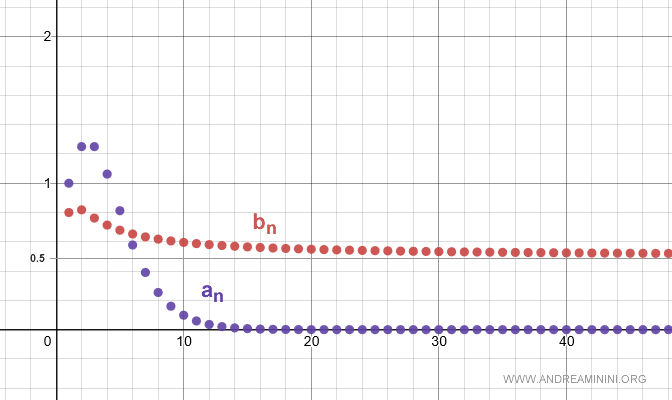
Below is a graphical representation of the two sequences.

Proof

Let’s consider a monotonic sequence a_n whose terms are all positive.

$$ a_n $$

We define a new sequence as the ratio of consecutive terms of a_n:

$$ b_n = \frac{a_{n+1}}{a_n} $$

By hypothesis, the limit of b_n is strictly less than 1:

$$ \lim_{n \rightarrow ∞} b_n < 1 $$

This implies that the limit of (1 - b_n) is greater than zero:

$$ \lim_{n \rightarrow ∞} (1-b_n) > 0 $$

According to the permanence of sign theorem, there exists some index v such that b_n < 1 for all n > v.

$$ b_n = \frac{a_{n+1}}{a_n} < 1 $$

Which leads to:

$$ a_{n+1} < a_n $$

This shows that the sequence a_n is decreasing.

Note. The limit of (1 - b_n) can only be positive if b_n itself is less than 1.

Furthermore, based on our initial assumption, the sequence a_n is monotonic and all its terms are positive.

Since it’s decreasing, monotonic, and made up of positive terms, it’s also a bounded sequence because its limit cannot fall below zero.

Therefore, by the theorem for bounded monotonic sequences, a_n must converge to a finite limit.

This limit is non-negative because the sequence’s terms are all positive.

$$ \lim_{n \rightarrow ∞} a_n = l_a \ge 0 $$

In summary, the limit l_a exists, is finite, and is non-negative.

There are only two possible cases:

• The limit l_a is greater than zero
• The limit l_a equals zero

If, by contradiction, the limit were greater than zero (l_a > 0), then:

$$ \lim_{n \rightarrow ∞} a_n = l_a > 0 $$

The limit of the sequence b_n would be 1:

$$ \lim_{n \rightarrow ∞} b_n = \lim_{n \rightarrow ∞} \frac{a_{n+1}}{a_n} = \frac{ \lim_{n \rightarrow ∞} a_{n+1} }{ \lim_{n \rightarrow ∞} a_n } = \frac{l_a}{l_a} = 1 $$

But this contradicts our hypothesis because we know b_n must be less than 1:

$$ b_n = \frac{a_{n+1}}{a_n} < 1 $$

Therefore, by elimination, the only possibility is that the limit l_a is zero:

$$ \lim_{n \rightarrow ∞} a_n = l_a = 0 $$

And that completes the proof of the theorem.

And so on.