Limit of a Function
- The limit (l) of a function f(x) as x approaches x0
- convergent if l is a finite number
- divergent if l is infinite
- nonexistent if the function oscillates or the limit fails to exist at x0
$$ \lim_{x \rightarrow x_0} f(x) = l $$ can be classified as:
Here, x0 is an accumulation point of the domain of f(x), while l may be any real number, either finite or infinite.
Convergent Limit
A] When x0 is a finite number
The limit of a function f(x) as x approaches x0 in ℝ is equal to l
$$ \lim_{x \rightarrow x_0} f(x) = l $$ if and only if, for every ε > 0, there exists a δ > 0 such that:
$$ l - \epsilon < f(x) < l + \epsilon $$ for all x within the interval (x0 - δ, x0 + δ).
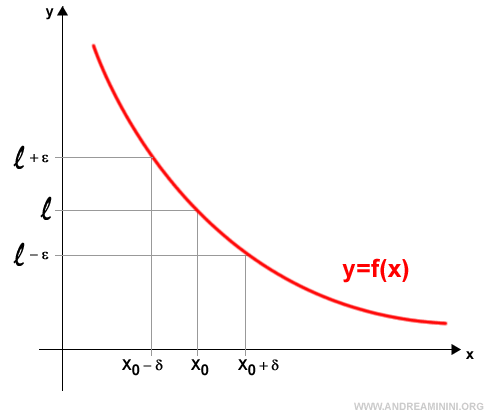
In this case, l is a finite real number.
In symbolic terms:
$$ \lim_{x \rightarrow x_0} f(x) = l \Leftrightarrow \forall \ \epsilon>0 \ , \ \exists \ \delta>0: |f(x)-l|<\epsilon \ , \ \forall \ x \in I: 0 \ne |x-x_0|<\delta $$
In other words, a function is said to have a real limit \( l \) as \( x \) approaches \( x_0 \) if, for every positive real number \( \epsilon \), there exists a punctured neighborhood \( I \) of \( x_0 \) such that \( |f(x) - l| < \epsilon \) for all \( x \in I \) with \( x \neq x_0 \).
The point \( x_0 \) is an accumulation point and, as such, it may or may not belong to the neighborhood \( I \).
Therefore, a function \( f(x) \) can have a finite real limit \( l \) at a point \( x_0 \) even if it is not defined at \( x_0 \).
Note. The limit of a function can also be characterized using subsequences. The limit of f(x) as x → x0 converges to the finite number l within a neighborhood A - {x0} if, for every subsequence xn contained in A and converging to x0, we have f(xn) = l.
B] When x0 approaches positive or negative infinity
The limit of a function f(x) as x tends to infinity is equal to the finite limit l
$$ \lim_{x \rightarrow \infty} f(x) = l $$ if and only if, for every ε > 0, there exists a number k > 0 such that:
$$ |f(x) - l| < \epsilon $$ for all x > k.
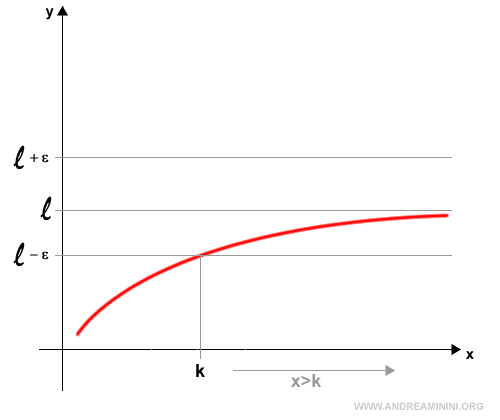
Here, l is a finite real number.
Symbolically:
$$ \lim_{x \rightarrow \infty} f(x) = l \Leftrightarrow \forall \epsilon>0, \exists k>0: |f(x)-l|<\epsilon, \forall x>k $$
The definition is analogous for x approaching -∞.
Example. Consider the function f(x) = 1/x. We compute its limit as x → ∞:
$$ \lim_{x \rightarrow +\infty} \frac{1}{x} = 0 $$
Divergent Limit to Infinity
A] If x0 is a finite number
The limit of a function as x→x0 diverges to positive infinity $$ \lim_{x \rightarrow x_0} f(x) = +∞ $$ if, for every real number M>0, there exists a number δ>0 such that the function f(x) takes values greater than M for all x in the neighborhood x0-δ<x<x0+δ.
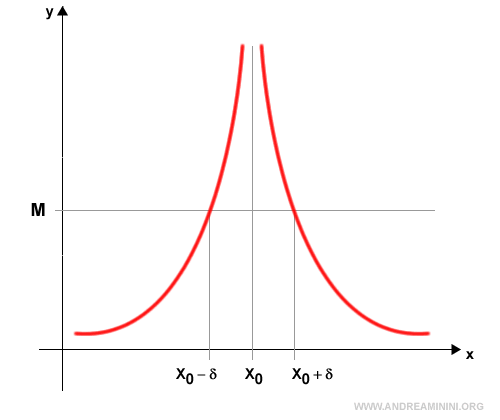
In symbolic form $$ \lim_{x \rightarrow x_0} f(x) = +∞ \Leftrightarrow \forall M>0, \exists δ>0: f(x)>M, \forall x \in A: 0 \ne |x-x_0|<δ $$ In other words, once x is restricted to a sufficiently small neighborhood of $ x_0 $, the values of the function $ f(x) $ eventually exceed any given positive bound.
The limit may diverge either to positive infinity (+∞) or to negative infinity (-∞).
The function f(x) diverges to negative infinity $$ \lim_{x \rightarrow x_0} f(x) = -∞ $$ if, for every real number M>0, there exists a number δ>0 such that the function f(x) takes values less than -M for all x in the neighborhood x0-δ<x<x0+δ.

In symbolic form
$$ \lim_{x \rightarrow x_0} f(x) = -∞ \Leftrightarrow \forall M>0, \exists δ>0: f(x)<-M, \forall x \in A: 0 \ne |x-x_0|<δ $$
In other words, when x is taken sufficiently close to $ x_0 $, the values of the function $ f(x) $ eventually fall below any prescribed negative bound.
Example. Given the function f(x)=1/((x-1)^2), compute the limit as x→1. $$ \lim_{x \rightarrow 1} \frac{1}{(x-1)^2} = +∞ $$
B] If x tends to positive or negative infinity
The limit of a function as x→+∞ diverges to positive infinity $$ \lim_{x \rightarrow +∞} f(x) = +∞ $$ if, for every real number M>0, there exists a number k>0 such that f(x) takes values greater than M for all x>k.
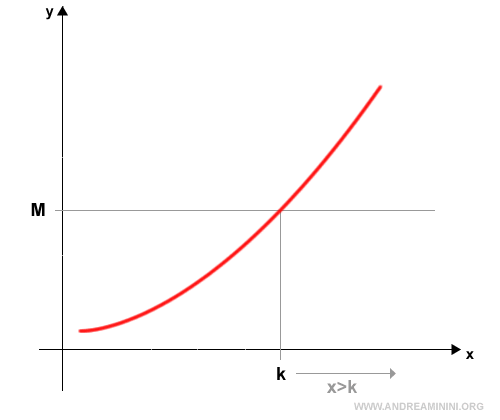
In symbolic form $$ \lim_{x \rightarrow +∞} f(x) = +∞ \Leftrightarrow \forall M>0, \exists k>0: f(x)>M, \forall x>k $$ In other words, as $ x $ grows without bound, the function eventually exceeds any prescribed positive bound and continues to increase indefinitely.
The limit may diverge either to positive infinity (+∞) or to negative infinity (-∞).
The limit of a function as x→+∞ diverges to negative infinity $$ \lim_{x \rightarrow +∞} f(x) = -∞ $$ if, for every real number M>0, there exists a number k>0 such that f(x) takes values less than -M for all x>k.
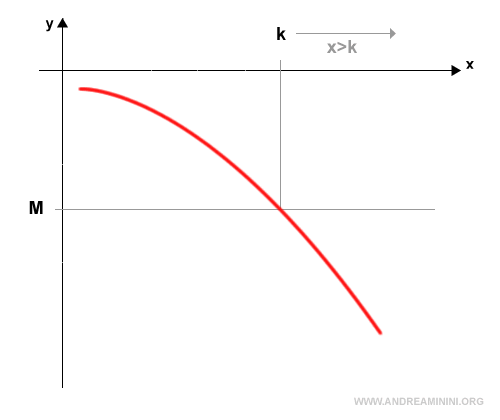
In symbolic form $$ \lim_{x \rightarrow +∞} f(x) = -∞ \Leftrightarrow \forall M>0, \exists k>0: f(x)<-M, \forall x>k $$
In other words, as $ x $ increases without bound, the function eventually falls below any prescribed negative bound and continues to decrease without any lower limit.
Example. Given the function f(x)=x2, compute the limit as x→+∞. $$ \lim_{x \rightarrow +∞} x^2 = +∞ $$
In these examples, only the case in which x tends to positive infinity has been considered. The definition of the limit as x→-∞ is completely analogous.
Nonexistent Limit
A] When x0 is a finite number
The limit of a function as x approaches x0 does not exist if the right-hand and left-hand limits are not equal:
$$ \lim_{ x \rightarrow x_0^+ } f(x) \ne \lim_{ x \rightarrow x_0^- } f(x) $$
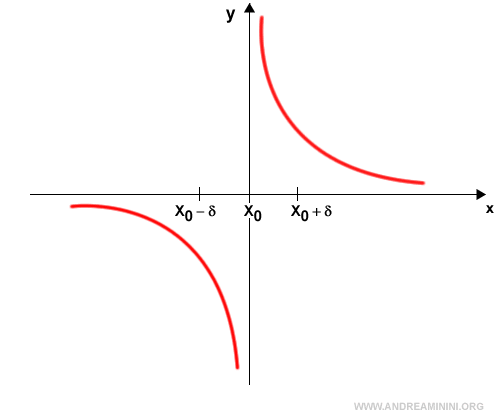
In such situations, the function might be undefined at x0 or possess a vertical asymptote there.
B] When x0 approaches positive or negative infinity
The limit of a function as x → ±∞ does not exist if the function oscillates indefinitely or is undefined:
$$ \lim_{ x \rightarrow \pm \infty } f(x) = \text{does not exist} $$
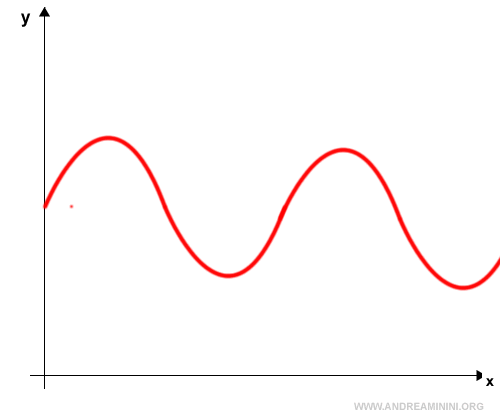
Examples
Consider the function:
$$ f(x) = \frac{1}{x} $$
The limit of this function as x → 0 does not exist:
$$ \lim_{ x \rightarrow 0 } \frac{1}{x} = \text{does not exist} $$
because the right-hand limit is +∞:
$$ \lim_{ x \rightarrow 0^+ } \frac{1}{x} = +\infty $$
while the left-hand limit is -∞:
$$ \lim_{ x \rightarrow 0^- } \frac{1}{x} = -\infty $$
The function 1/x is undefined at x0 = 0, where it has a vertical asymptote.
And so forth.
