Continuity Theorem for Inverse Functions

A function f(x) that is strictly monotonic over a closed interval [a,b] is continuous if and only if its inverse function f^-1(x) is continuous.

A Practical Example

Consider the following function, which is strictly increasing on the closed interval [-2,2]:

$$ y = f(x) = 2x $$

This function is invertible, and its inverse is given by:

$$ x = f^{-1}(y) = \frac{y}{2} $$

Here’s its graph on the Cartesian plane:

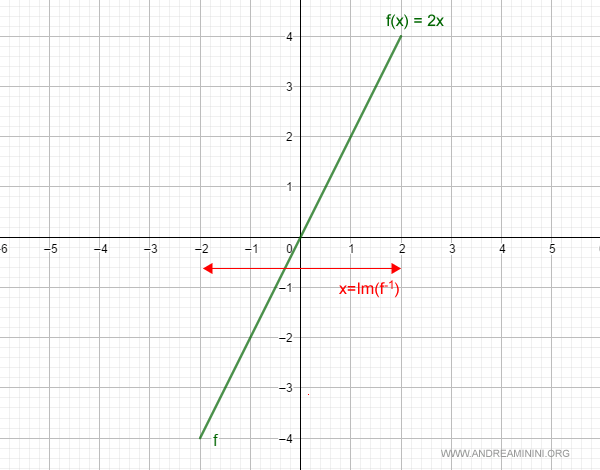
To determine whether f(x) is continuous, we apply the continuity criterion for monotonic functions to its inverse.

Note. According to the continuity criterion for monotonic functions, a function is continuous if its image Im(f) contains every value between its endpoints f(a) and f(b) over the interval [a,b].

In this case, the function under consideration is:

$$ f^{-1}(y) = \frac{y}{2} $$

The domain of the inverse function f^-1 is:

$$ y \in [-4,4] $$

The values of the inverse function at the endpoints are:

$$ f^{-1}(-4) = -2 \\ f^{-1}(4) = 2 $$

Therefore, the image of the inverse function (i.e. its codomain) is:

$$ Im(f^{-1}) = [-2,2] $$

The image of f^-1 spans all values between f^-1(-4) and f^-1(4).

Hence, by the theorem, the strictly monotonic function f(x) = 2x is continuous.

Proof Explained

A strictly monotonic function f(x) defined over a closed interval [a,b] is always invertible.

As such, it necessarily has an inverse function f^-1(y):

$$ y = f(x) $$

$$ x = f^{-1}(y) \quad \text{(inverse function)} $$

Note. A function is strictly monotonic if it is either strictly increasing or strictly decreasing throughout the entire interval. Unlike functions that are merely monotonic, a strictly monotonic function can never remain constant over any portion of its domain.

Two scenarios are possible:

• If f(x) is strictly increasing on [a,b]: $$ f:[a,b] \rightarrow [f(a), f(b)] $$ $$ f^{-1}:[f(a), f(b)] \rightarrow [a,b] $$
• If f(x) is strictly decreasing on [a,b]: $$ f:[a,b] \rightarrow [f(b), f(a)] $$ $$ f^{-1}:[f(b), f(a)] \rightarrow [a,b] $$

In both situations, the image Im(f) covers the entire range of values between f(a) and f(b).

Therefore, the inverse function f^-1(y) is continuous.

Note. According to the continuity criterion for monotonic functions, a monotonic function is continuous if its image Im(f) encompasses all values between f(a) and f(b).

Thus, if the inverse function f^-1(x) is continuous, then the original strictly monotonic function f(x) must also be continuous.

And so on.