How to Analyze a Function

Analyzing a function f(x) allows us to sketch its graph by examining its domain, sign, and first and second derivatives.

Let’s take the following function as an example:

$$ f(x)= \frac{x}{x-1} $$

To draw its graph, I follow these steps:

Determining the Domain

The first step in analyzing a function is to identify its domain - the set of x-values for which the function is defined.

For the function f(x) = x / (x - 1), the domain is:

$$ ( -\infty, 1) \cup (1, \infty ) \:\:\:\: \forall x \in R $$

This also highlights the points where the function is undefined.

In this case, f(x) = x / (x - 1) is undefined at x = 1:

$$ f(1)= \frac{1}{1-1} |_{x=1} = \frac{1}{0} \:\:\: undefined $$

Such undefined points may indicate the presence of vertical asymptotes.

Analyzing the Sign of the Function

Next, I determine whether the function is positive or negative within its domain.

Here, the function is positive on the intervals (-\infty, 0) and (1, \infty), and negative on (0, 1).

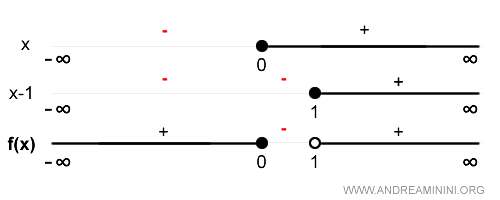
This step reveals which quadrants of the Cartesian plane the function occupies.

Quadrants where the function does not appear can be disregarded.

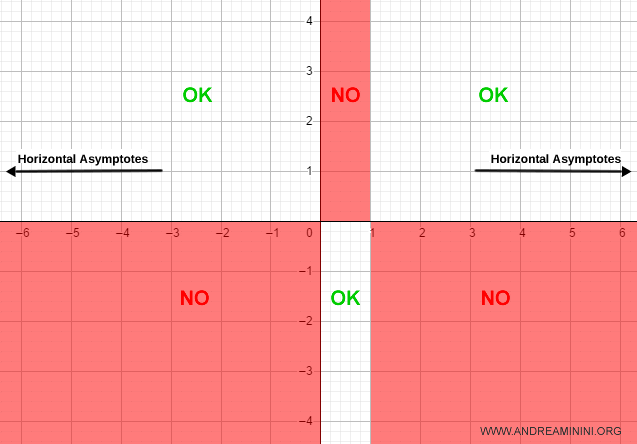
Horizontal Asymptotes

To find horizontal asymptotes, I calculate the limits of the function as x approaches positive and negative infinity - that is, at the edges of the domain.

$$ \lim_{x \rightarrow \infty}{ \frac{x}{x-1} } = \frac{\infty}{\infty} $$

$$ \lim_{x \rightarrow -\infty}{ \frac{x}{x-1} } = \frac{\infty}{\infty} $$

These are indeterminate forms.

To resolve them, I apply L'Hôpital’s Rule:

$$ \lim_{x \rightarrow \infty}{ \frac{D[x]}{D[x-1]} } = \lim_{x \rightarrow \infty}{ \frac{1}{1} } = 1 $$

$$ \lim_{x \rightarrow -\infty}{ \frac{D[x]}{D[x-1]} } = \lim_{x \rightarrow -\infty}{ \frac{1}{1} } = 1 $$

Since both limits yield finite results, the function has two horizontal asymptotes at y = 1 as x approaches ±∞:

$$ \lim_{x \rightarrow \infty}{ \frac{x}{x-1} } = 1 $$

$$ \lim_{x \rightarrow -\infty}{ \frac{x}{x-1} } = 1 $$

I now add these asymptotes to the graph:

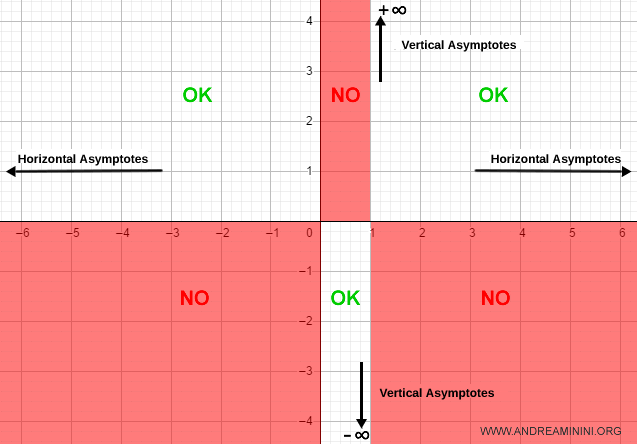
Vertical Asymptotes

For any undefined points within the domain, I calculate the limits as x approaches these points from the left and right.

Here, the function is undefined at x = 1:

$$ \lim_{x \rightarrow 1^+}{ \frac{x}{x-1} } = \frac{1}{0^+} = \infty $$

$$ \lim_{x \rightarrow 1^-}{ \frac{x}{x-1} } = \frac{1}{0^-} = -\infty $$

This means that as x approaches 1 from the right, the function tends toward +∞; from the left, it tends toward -∞.

I add the vertical asymptote to the graph:

Oblique Asymptotes

When x approaches ±∞, I can check for the presence of an oblique (slant) asymptote of the form mx + q by evaluating the following limits:

$$ m = \lim_{x \rightarrow \infty } \frac{f(x)}{x} =\lim_{x \rightarrow \infty } \frac{\frac{x}{x-1}}{x} = 0 $$

$$ q = \lim_{x \rightarrow \infty } [f(x) - mx] = \lim_{x \rightarrow \infty } \left( \frac{x}{x-1} - 0 \cdot x \right) = 1 $$

If these limits exist and are finite, and m ≠ 0, an oblique asymptote of the form mx + q is present.

In this case, since m = 0, there is no oblique asymptote as x → ±∞.

Note. For this function f(x), the slope m = 0 and q = 1 - a result that matches the previously found horizontal asymptotes. Therefore, no oblique asymptote exists.

Symmetry Analysis

I begin by checking whether the function exhibits any symmetry.

For example, whether it is an even function:

$$ f(-x) = f(x) $$

or an odd function:

$$ f(-x) = -f(x) $$

In this case, the function x / (x - 1) does not display any symmetry.

Periodicity

Next, I check whether the function is periodic with period T:

$$ T: f(x+T) = f(x) \:\:\:\: \forall x \in R $$

For instance, the sine function is periodic with period T = 2π.

If the function is periodic, it is sufficient to study its behavior over a single period T, and then extend the results across all intervals (T+1, T+2, ...).

In this particular case, the function x / (x - 1) is not periodic.

Intercepts with the Axes

Finding the x- and y-intercepts provides valuable information for constructing the graph.

Y-intercept

By setting x = 0, I can determine the corresponding y-value:

$$ y = \frac{x}{x-1}|_{x=0} = \frac{0}{0-1} = 0 $$

Thus, the function intersects the y-axis at the origin (0, 0).

X-intercept

If convenient, I also calculate the x-intercept by setting y = 0:

$$ \frac{x}{x-1} = 0 $$

Note. In this case, the x-intercept coincides with the y-intercept at the origin (0, 0). This is not always true - the two intercepts may be distinct, or may not exist at all.

Therefore, the function passes through the point P(0, 0).

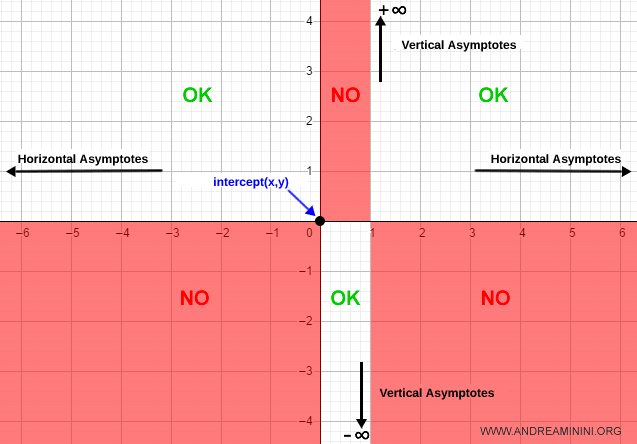
Intervals of Increase and Decrease

To determine where the function is increasing or decreasing, I calculate its first derivative:

$$ f'(x) = D\left[ \frac{x}{x-1} \right] = \frac{(x-1)-x}{(x-1)^2} = \frac{-1}{(x-1)^2} $$

I then examine the sign of the first derivative:

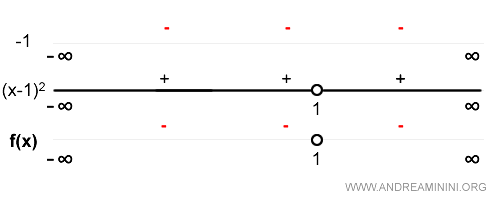
The function is increasing where f'(x) > 0, and decreasing where f'(x) < 0.

In this case, the function is decreasing throughout its entire domain.

On the interval (-\infty, 0), the function decreases from the horizontal asymptote at y = 1 toward the origin.

On the interval (0, 1), the function passes through the origin and decreases toward negative infinity.

On the interval (1, \infty), the function decreases from the vertical asymptote toward the horizontal asymptote at y = 1.

Note. These observations allow me to exclude regions of the Cartesian plane where the function cannot appear.

Local Minima and Maxima

I then look for critical points x₀ where the first derivative is zero, to identify any local minima or maxima:

$$ f'(x_0) = 0 $$

At such points:

• Local maximum: if the function is increasing to the left of x₀ ( f'(x) > 0 ) and decreasing to the right ( f'(x) < 0 ).
• Local minimum: if the function is decreasing to the left of x₀ ( f'(x) < 0 ) and increasing to the right ( f'(x) > 0 ).

In all other cases, the function has neither a local minimum nor a maximum at x₀.

For this function, the first derivative is never zero:

$$ f'(x) = \frac{-1}{(x-1)^2} \ne 0 \:\:\:\: \forall x \in R $$

Therefore, there are no local minima or maxima in the domain.

Inflection Points

I also check for potential inflection points, which occur where the first derivative equals zero:

$$ f'(x_0) = 0 $$

An inflection point occurs if the function is increasing or decreasing on both sides of x₀, with a change in concavity.

To distinguish between an upward and downward inflection point, I calculate the second derivative:

If:

$$ f''(x_0) = 0 $$

Then:

• Upward inflection point: if f''(x) changes from negative to positive near x₀ (from concave down to concave up).
• Downward inflection point: if f''(x) changes from positive to negative near x₀ (from concave up to concave down).

For this function, the first derivative is never zero:

$$ f'(x) = \frac{-1}{(x-1)^2} \ne 0 \:\:\:\: \forall x \in R $$

Therefore, there are no inflection points in the domain.

Concavity and Convexity

Finally, I calculate the second derivative to identify intervals of concavity and convexity:

$$ D^2[ f(x) ] = D\left[ \frac{-1}{(x-1)^2} \right] = \frac{ 2(x-1)}{(x-1)^4} = \frac{2}{(x-1)^3} $$

I then analyze the sign of the second derivative:

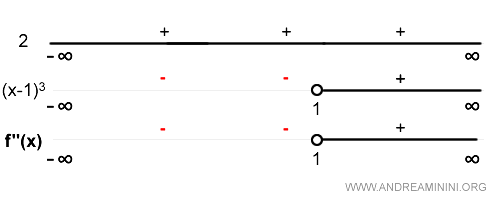
The function is:

• convex where f''(x) ≥ 0,
• concave where f''(x) ≤ 0.

Therefore, the function f(x) = x / (x - 1) is concave on the interval (-\infty, 1), and convex on (1, \infty).

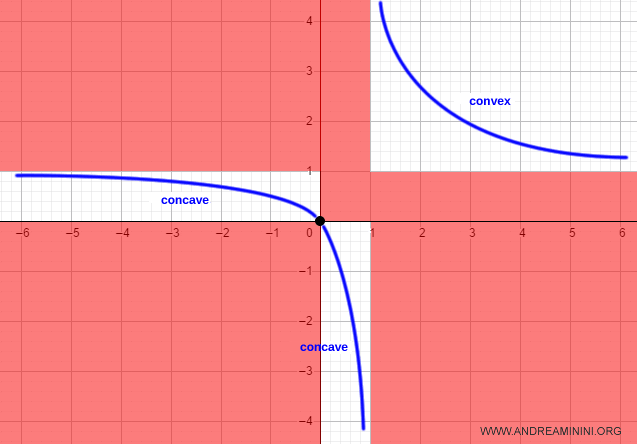
This completes the graph and full analysis of the function.

And so on.