Worked Example Function Analysis 3

In this example, we will analyze the following function:

$$ f(x) = \frac{x^2 + 2}{x} $$

Domain

The function is defined for all real numbers except $ x = 0 $, where the denominator vanishes:

$$ D_f = (-\infty, 0) \cup (0, +\infty) $$

Undefined Points

The point $ x = 0 $ is undefined and corresponds to a vertical asymptote.

Let us compute the one-sided limits:

$$ \lim_{x \to 0^+} \frac{x^2 + 2}{x} = +\infty $$

$$ \lim_{x \to 0^-} \frac{x^2 + 2}{x} = -\infty $$

Thus, as $ x \to 0 $, the function tends to $ +\infty $ from the right and $ -\infty $ from the left:

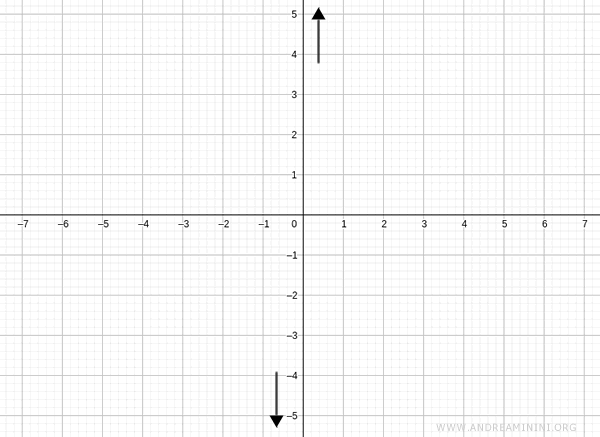
vertical asymptote at x = 0

Asymptotic Behavior

We now examine the limits as $ x \to +\infty $ and $ x \to -\infty $:

$$ \lim_{x \to +\infty} \frac{x^2 + 2}{x} = +\infty $$

$$ \lim_{x \to -\infty} \frac{x^2 + 2}{x} = -\infty $$

Therefore, as $ x \to +\infty $, $ f(x) \to +\infty $, and as $ x \to -\infty $, $ f(x) \to -\infty $:

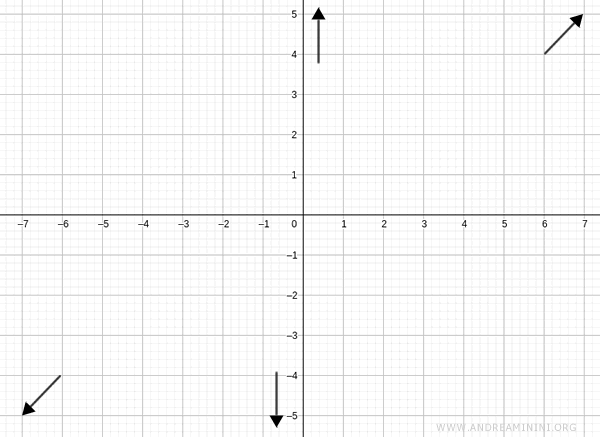
asymptotic behavior at infinity

Intercepts with the Axes

At $ x = 0 $, the function is undefined:

$$ f(0) = \frac{0^2 + 2}{0} $$

To find any x-intercepts, we solve:

$$ \frac{x^2 + 2}{x} = 0 $$

Multiplying both sides by $ x $:

$$ x^2 + 2 = 0 $$

$$ x^2 = -2 $$

This equation has no real solutions. Thus, the graph does not intersect the x-axis.

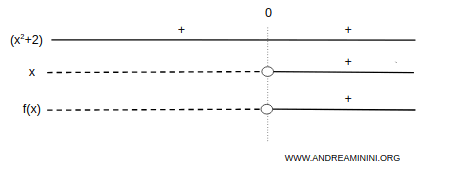
Sign Analysis

The function is negative on $ (-\infty, 0) $, and positive on $ (0, +\infty) $:

sign analysis

We can therefore exclude regions of the plane where the function does not take any values (shaded regions):

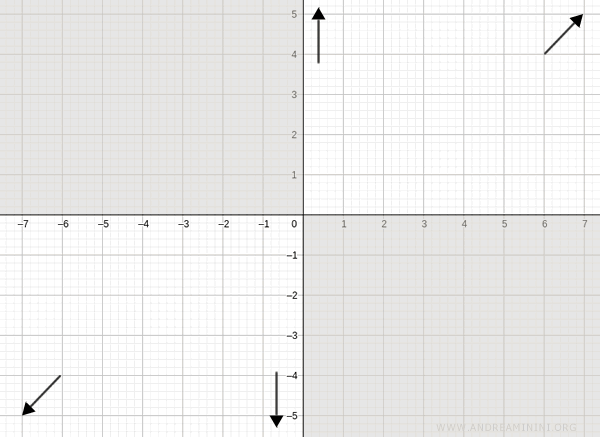
shaded regions

Monotonicity

We compute the first derivative:

$$ f'(x) = D\left[ \frac{x^2 + 2}{x} \right] = \frac{2x \cdot x - (x^2 + 2)}{x^2} = \frac{x^2 - 2}{x^2} $$

We analyze the sign of $ f'(x) $:

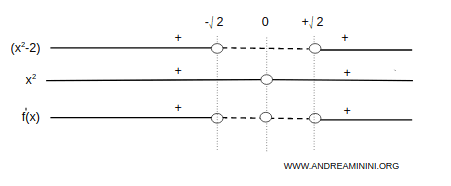
first derivative sign analysis

The function is increasing on $ (-\infty, -\sqrt{2}) $ and $ (\sqrt{2}, +\infty) $, and decreasing on $ (-\sqrt{2}, \sqrt{2}) $:

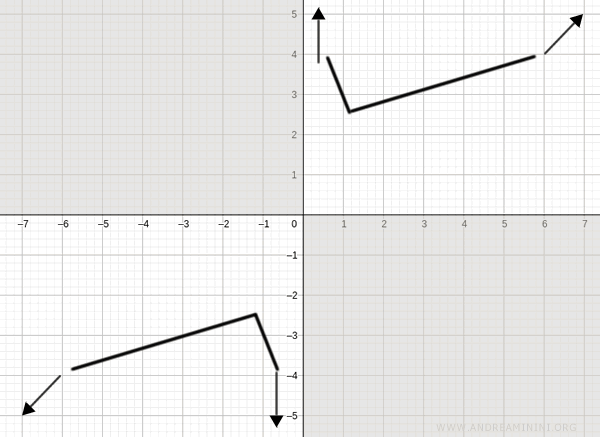
monotonicity

At $ x = -\sqrt{2} $, the function has a local maximum, since $ f'(x) = 0 $ and the derivative changes from positive to negative:

$$ \left( -\sqrt{2}, f(-\sqrt{2}) \right) = \left( -\sqrt{2}, \frac{(-\sqrt{2})^2 + 2}{-\sqrt{2}} \right) = \left( -\sqrt{2}, -\frac{4}{\sqrt{2}} \right) $$

At $ x = \sqrt{2} $, the function has a local minimum, since $ f'(x) = 0 $ and the derivative changes from negative to positive:

$$ \left( \sqrt{2}, f(\sqrt{2}) \right) = \left( \sqrt{2}, \frac{(\sqrt{2})^2 + 2}{\sqrt{2}} \right) = \left( \sqrt{2}, \frac{4}{\sqrt{2}} \right) $$

Concavity and Convexity

We now compute the second derivative:

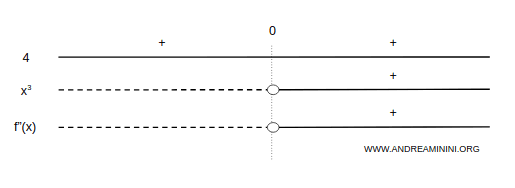
$$ f''(x) = D\left[ \frac{x^2 - 2}{x^2} \right] $$

$$ = \frac{2x(x^2) - (x^2 - 2)(2x)}{x^4} = \frac{4x}{x^4} = \frac{4}{x^3} $$

The function is concave on $ (-\infty, 0) $, and convex on $ (0, +\infty) $:

concavity and convexity

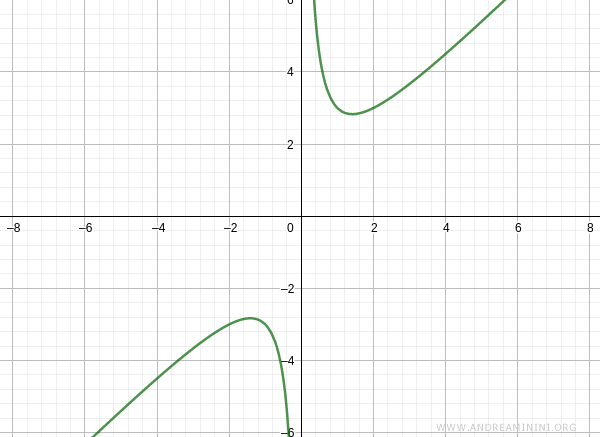
The graph of the function therefore takes the following shape:

graph of the function

Oblique Asymptotes

We now investigate the existence of oblique asymptotes.

First, we compute the slope $ m $:

$$ m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x^2 + 2}{x^2} = 1 $$

Since $ m $ is finite, we compute $ q $:

$$ q = \lim_{x \to +\infty} \left( f(x) - m x \right) = \lim_{x \to +\infty} \left( \frac{x^2 + 2}{x} - x \right) = \lim_{x \to +\infty} \frac{2}{x} = 0 $$

Thus, the function has an oblique asymptote as $ x \to +\infty $, given by:

$$ y = x $$

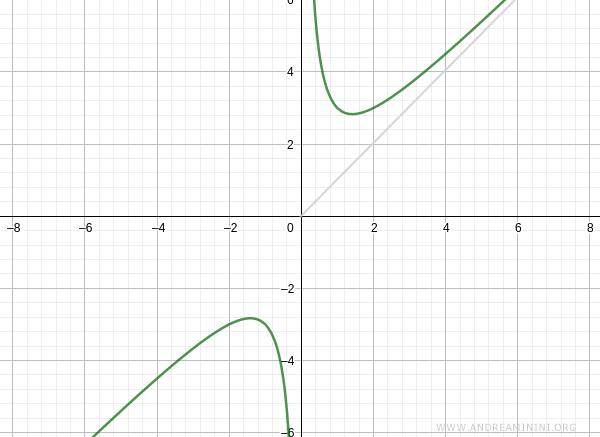
oblique asymptote

Repeating the same analysis as $ x \to -\infty $:

$$ m = \lim_{x \to -\infty} \frac{f(x)}{x} = 1 $$

$$ q = \lim_{x \to -\infty} \left( f(x) - m x \right) = \lim_{x \to -\infty} \frac{2}{x} = 0 $$

Thus, the oblique asymptote is again:

$$ y = x $$

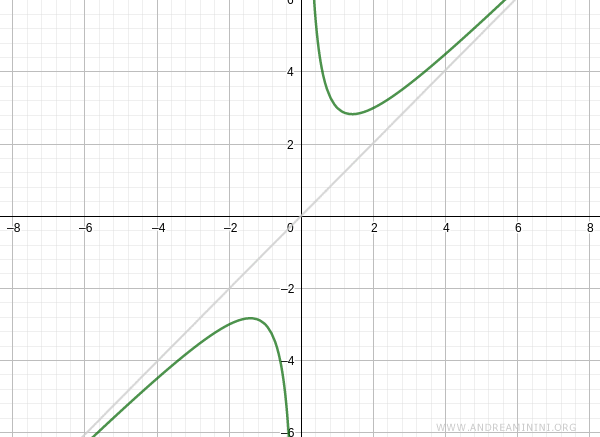
oblique asymptote

And so on.