Worked Example - Function Analysis 4

In this example, we will analyze the following function:

$$ f(x) = \frac{x}{x^2 + 2} $$

Domain

The function is defined for all real numbers:

$$ D_f = (-\infty, +\infty) $$

Undefined Points

The function is defined everywhere, as the denominator $ x^2 + 2 $ has no real roots:

$$ x^2 + 2 = 0 \quad \Rightarrow \quad x^2 = -2 $$

Asymptotic Behavior

We now analyze the behavior of the function as $ x \to \pm\infty $:

$$ \lim_{x \to +\infty} \frac{x}{x^2 + 2} = 0^+ $$

$$ \lim_{x \to -\infty} \frac{x}{x^2 + 2} = 0^- $$

Thus, the function approaches zero from above as $ x \to +\infty $, and from below as $ x \to -\infty $:

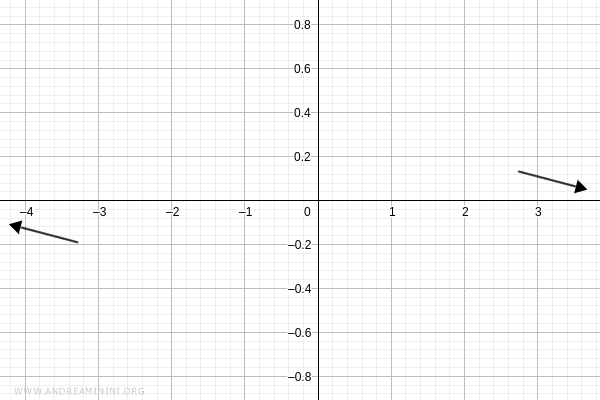
asymptotic behavior

Intercepts with the Axes

At $ x = 0 $, the function evaluates to:

$$ f(0) = \frac{0}{0^2 + 2} = 0 $$

Thus, the graph passes through the origin $ (0, 0) $:

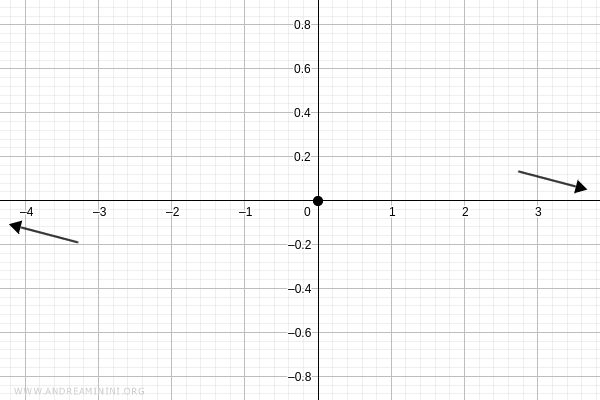
intercept at origin

Sign Analysis

The function is negative on $ (-\infty, 0) $, and positive on $ (0, +\infty) $:

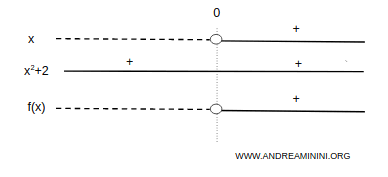
sign analysis

We can therefore exclude from the graph those regions of the plane where the function does not take any values:

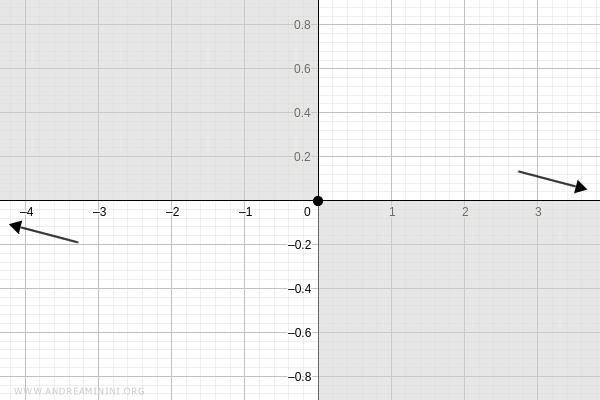
excluded regions

Monotonicity

We compute the first derivative:

$$ f'(x) = D\left[ \frac{x}{x^2 + 2} \right] = \frac{(x^2 + 2) - x(2x)}{(x^2 + 2)^2} = \frac{-x^2 + 2}{(x^2 + 2)^2} $$

Analyzing the sign of $ f'(x) $, we find:

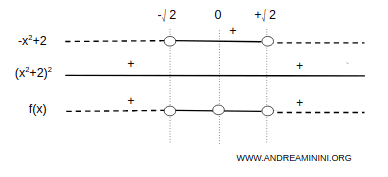
first derivative sign analysis

The function is increasing on $ (-\sqrt{2}, \sqrt{2}) $, and decreasing on $ (-\infty, -\sqrt{2}) $ and $ (\sqrt{2}, +\infty) $:

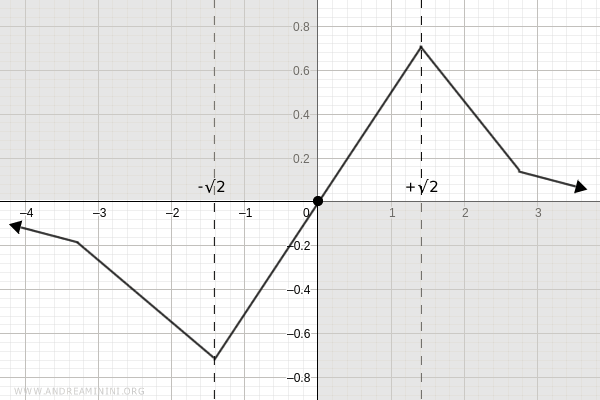
monotonicity

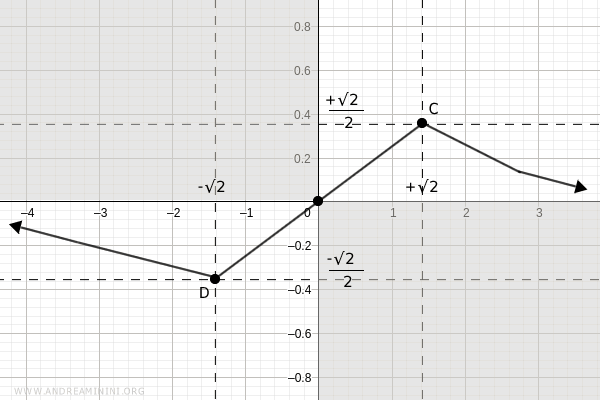
There is a local minimum at $ x = -\sqrt{2} $, and a local maximum at $ x = \sqrt{2} $:

$$ C: \ (x, y) = \left( \sqrt{2}, \frac{ \sqrt{2} }{ (\sqrt{2})^2 + 2 } \right) = \left( \sqrt{2}, \frac{ \sqrt{2} }{4} \right) $$

$$ D: \ (x, y) = \left( -\sqrt{2}, \frac{ -\sqrt{2} }{ (\sqrt{2})^2 + 2 } \right) = \left( -\sqrt{2}, -\frac{ \sqrt{2} }{4} \right) $$

This allows us to refine the graph accordingly:

refined graph

Concavity and Convexity

Next, we compute the second derivative to analyze the concavity of the graph:

$$ f''(x) = D\left[ \frac{ -x^2 + 2 }{ (x^2 + 2)^2 } \right] $$

$$ = \frac{ -2x(x^2 + 2)^2 - 2(x^2 + 2)(-x^2 + 2)(2x) }{ (x^2 + 2)^4 } $$

$$ = \frac{ -2x(x^2 + 2) - 4x(-x^2 + 2) }{ (x^2 + 2)^3 } $$

$$ = \frac{ -2x^3 - 4x + 4x^3 - 8x }{ (x^2 + 2)^3 } $$

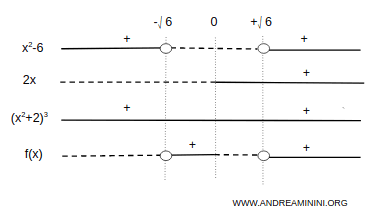
$$ = \frac{ 2x(x^2 - 6) }{ (x^2 + 2)^3 } $$

From this, we see that the function is concave on $ (-\infty, -\sqrt{6}) $ and $ (0, \sqrt{6}) $, and convex on $ (-\sqrt{6}, 0) $ and $ (\sqrt{6}, +\infty) $:

concavity and convexity

The graph of the function is thus as follows:

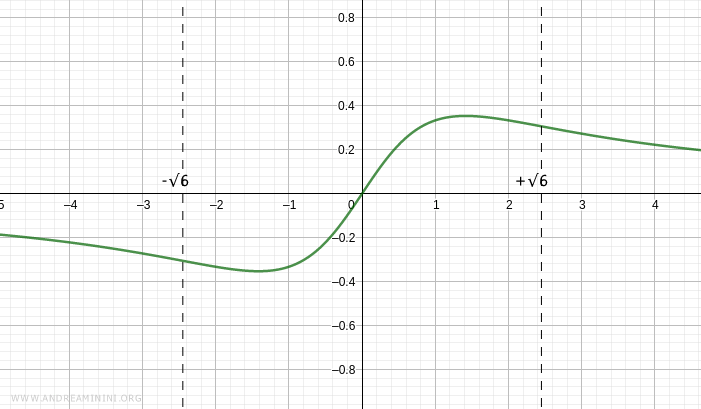
graph of the function

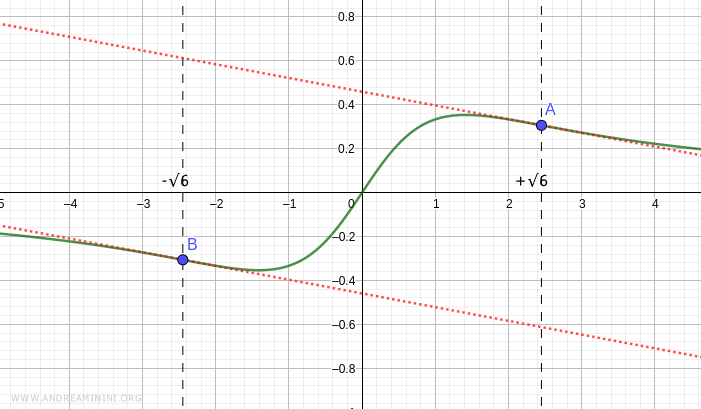
There are two inflection points at $ x = -\sqrt{6} $ and $ x = \sqrt{6} $:

$$ A: \ (x, y) = \left( \sqrt{6}, \frac{ \sqrt{6} }{ (\sqrt{6})^2 + 2 } \right) = \left( \sqrt{6}, \frac{ \sqrt{6} }{8} \right) $$

$$ B: \ (x, y) = \left( -\sqrt{6}, \frac{ -\sqrt{6} }{ (\sqrt{6})^2 + 2 } \right) = \left( -\sqrt{6}, -\frac{ \sqrt{6} }{8} \right) $$

Graphically, these appear as follows:

inflection points

And so on.