Minimum and Maximum of a Function

According to Fermat’s Theorem, if a function is defined on the interval [a, b] and has a local minimum or maximum at the point x₀, then its first derivative at that point is zero. $$ f'(x_0)=0 $$

Therefore, to find local minima or maxima, we follow these steps:

1. Calculate the first derivative of the function f(x).
2. Find the points where the first derivative equals zero, i.e., solve f'(x)=0.

This approach applies only if the function is differentiable on [a, b].

Once we’ve identified the points where the first derivative is zero - say, x₀ - we need to determine whether those points correspond to minima or maxima.

How to Determine Whether It’s a Maximum or Minimum

There are several ways to proceed:

1. Analyze whether the first derivative f'(x) is increasing or decreasing around x₀.
   • If the first derivative is increasing near x₀, then x₀ is a local minimum.
   • If the first derivative is decreasing near x₀, then x₀ is a local maximum.
2. Calculate the second derivative f″(x) near x₀.
   • If the second derivative is greater than or equal to zero, the point is a local minimum. $$ f″(x_0) \ge 0 \Leftrightarrow \text{minimum} $$
   • If the second derivative is less than or equal to zero, the point is a local maximum. $$ f″(x_0) \le 0 \Leftrightarrow \text{maximum} $$

Note The derivative test can also be extended to higher even-order derivatives, provided that all the lower-order derivatives vanish. $$ f^{(k)} \ne 0 \quad \text{for even } k $$ $$ f^{(1)} = f^{(2)} = \ldots = f^{(k-1)} = 0 $$ This makes it a powerful tool in mathematical analysis and curve investigation. However, it requires the function to be continuous and differentiable at x₀.

The two methods above are equivalent, thanks to the monotonicity criterion.

• If the first derivative f'(x) is increasing around x₀, then the second derivative is necessarily nonnegative. $$ f'(x) \text{ increasing } \Leftrightarrow f″(x_0) \ge 0 $$
• If the first derivative f'(x) is decreasing around x₀, then the second derivative is necessarily nonpositive. $$ f'(x) \text{ decreasing } \Leftrightarrow f″(x_0) \le 0 $$

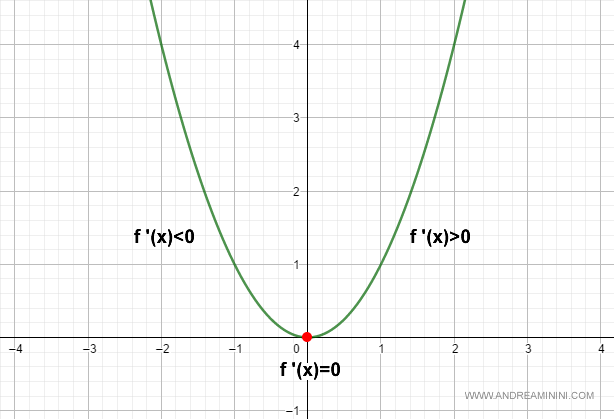
A Practical Example

Let’s find the extrema of the following function:

$$ f(x)=x^2 $$

First, we calculate the first derivative:

$$ f'(x)=2x $$

Next, we identify where the first derivative equals zero:

The first derivative is zero only at x=0:

$$ x=0 \rightarrow f'(0)=0 $$

We then compute the second derivative, which is the derivative of the first derivative:

$$ f″(x)=2 $$

Finally, we evaluate the second derivative at x=0:

$$ f″(0)=2 \ge 0 $$

Since the second derivative is positive, the function has a local minimum at x=0.

Proof

Consider a function that is defined and continuous on (a, b).

If its first derivative is zero at some point x₀ within (a, b):

$$ f'(x_0)=0 $$

Then, by Fermat’s Theorem, the function f(x) may have either a local minimum or a local maximum at x₀.

Note. However, this doesn’t guarantee the existence of a minimum or maximum - it could also be a point of inflection.

If the second derivative at x₀ is positive:

$$ f″(x_0) > 0 $$

Since the function is continuous, the theorem of permanence of sign ensures that there exists a neighborhood (x-δ, x+δ) where f″(x) > 0.

Therefore, in this interval, the first derivative f'(x) is increasing, and the function f(x) is convex.

When a function is convex, the tangent line at x₀ always lies below the graph of f(x):

$$ f(x) \ge f(x_0) + f'(x_0)(x - x_0) $$

Since f'(x₀)=0:

$$ f(x) \ge f(x_0) $$

This demonstrates that x₀ is a point of local minimum.

Note. The proof for a local maximum is similar, except that it starts with the assumption that the second derivative at x₀ is negative.

And so on.