Worked Example Function Analysis 2

We will analyze the graph of the following function:

$$ f(x) = \frac{x-1}{x+1} $$

Domain

The function is defined on the following domain:

$$ D_f = (-\infty, -1) \cup (-1, +\infty) \ \ \ \forall \ x \in \mathbb{R} $$

Sign Analysis

The function is positive on the intervals $ (-\infty, -1) \cup (1, +\infty) $, and negative on $ (-1, 1) $:

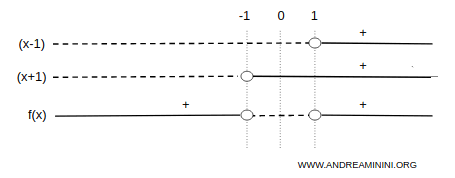
sign analysis of the function

This allows us to exclude the regions of the plane where the function does not take any values (shaded in gray):

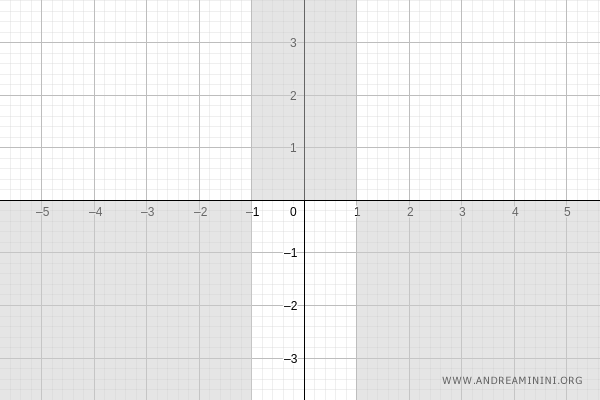
regions where the function is defined

Undefined Points

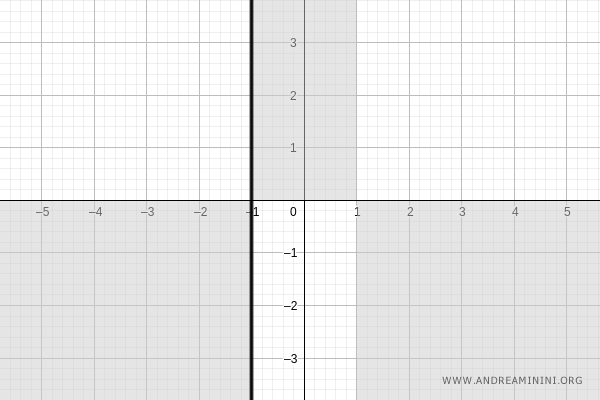
The function is undefined at $ x = -1 $, as the denominator vanishes at this point. Therefore, a vertical asymptote may occur:

undefined point

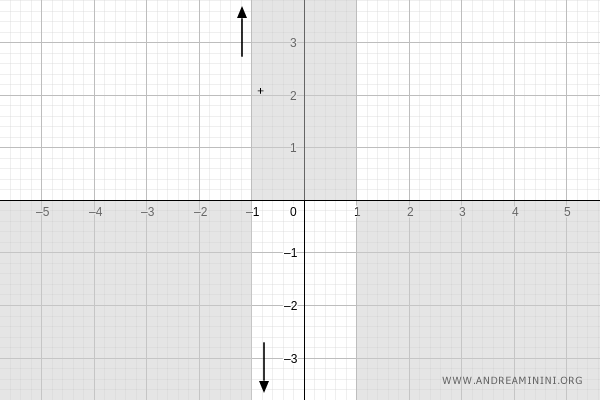
We compute the one-sided limits as $ x \to -1 $:

$$ \lim_{x \to -1^-} \frac{x-1}{x+1} = +\infty $$

$$ \lim_{x \to -1^+} \frac{x-1}{x+1} = -\infty $$

Thus, as $ x \to -1 $, the function tends to $ +\infty $ from the left and $ -\infty $ from the right:

vertical asymptote at x = -1

Intercepts with the Axes

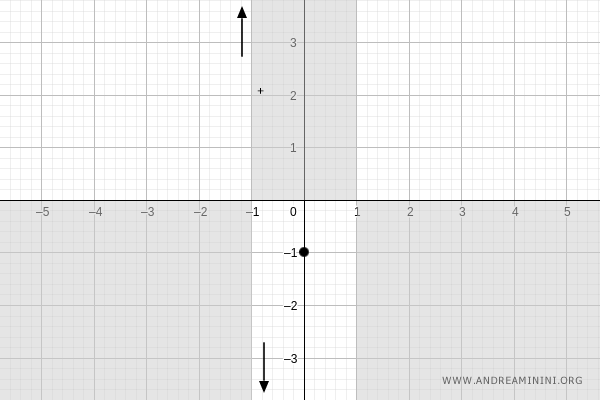
At $ x = 0 $, the function evaluates to:

$$ f(0) = \frac{0-1}{0+1} = -1 $$

Thus, the graph passes through the point $ (0, -1) $:

intercept at (0, -1)

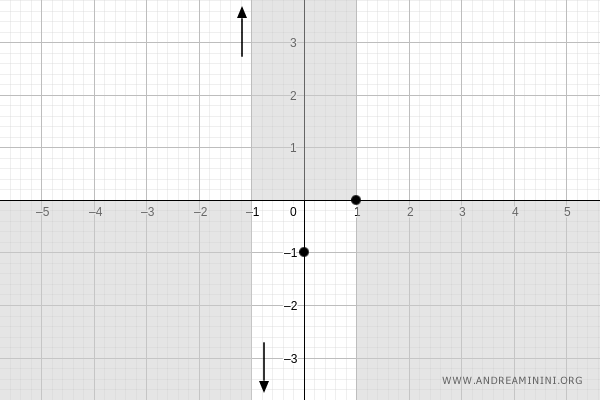
To find the x-intercept (where $ f(x) = 0 $), we solve:

$$ \frac{x-1}{x+1} = 0 $$

$$ x - 1 = 0 \quad \Rightarrow \quad x = 1 $$

Thus, the graph also passes through $ (1, 0) $:

intercept at (1, 0)

Horizontal Asymptotes

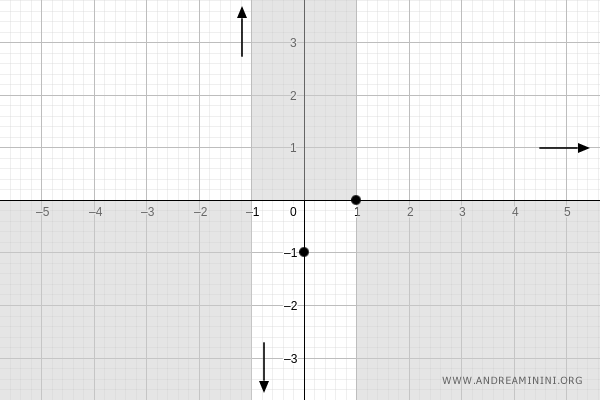
We now compute the limits as $ x \to +\infty $:

$$ \lim_{x \to +\infty} \frac{x-1}{x+1} = \frac{\infty}{\infty} $$

Since this is an indeterminate form $ \frac{\infty}{\infty} $, we apply L'Hôpital’s Rule:

$$ \lim_{x \to +\infty} \frac{D[x-1]}{D[x+1]} = \frac{1}{1} = 1 $$

Therefore, as $ x \to +\infty $, $ f(x) \to 1 $:

horizontal asymptote at y = 1

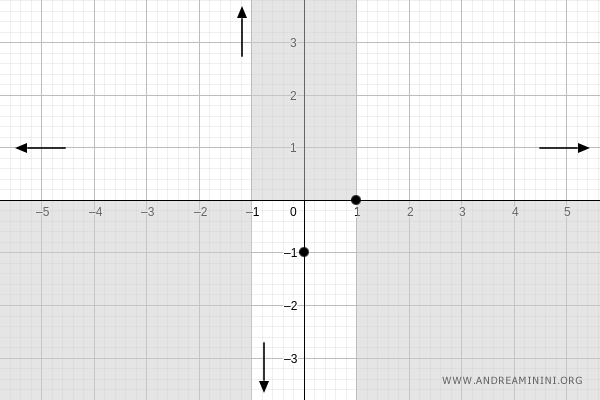
Similarly, as $ x \to -\infty $:

$$ \lim_{x \to -\infty} \frac{x-1}{x+1} = \frac{\infty}{\infty} $$

Applying L'Hôpital’s Rule again:

$$ \lim_{x \to -\infty} \frac{D[x-1]}{D[x+1]} = \frac{1}{1} = 1 $$

Thus, as $ x \to -\infty $, $ f(x) \to 1 $:

horizontal asymptote at y = 1 for x → -∞

Monotonicity (Increasing/Decreasing Behavior)

We now compute the first derivative:

$$ f'(x) = D\left[\frac{x-1}{x+1}\right] = \frac{(x+1) - (x-1)}{(x+1)^2} = \frac{2}{(x+1)^2} $$

Since $ f'(x) > 0 $ for all $ x \in D_f $, the function is strictly increasing:

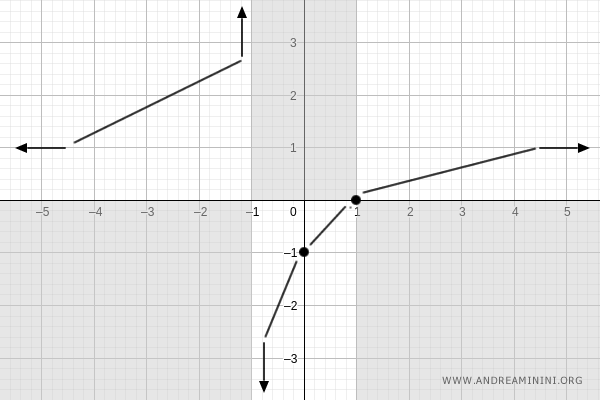
the function is increasing

Concavity and Convexity

Next, we compute the second derivative:

$$ f''(x) = D\left[ \frac{2}{(x+1)^2} \right] = -4(x+1)^{-3} = \frac{-4}{(x+1)^3} $$

The second derivative is positive on $ (-\infty, -1) $, and negative on $ (-1, +\infty) $:

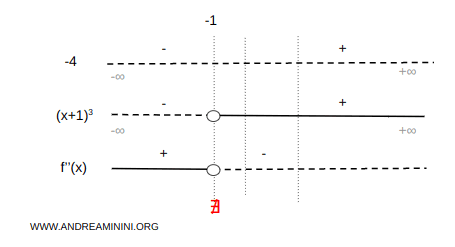
second derivative sign analysis

Thus:

The function is convex on $ (-\infty, -1) $.
The function is concave on $ (-1, +\infty) $.

We update the graph accordingly:

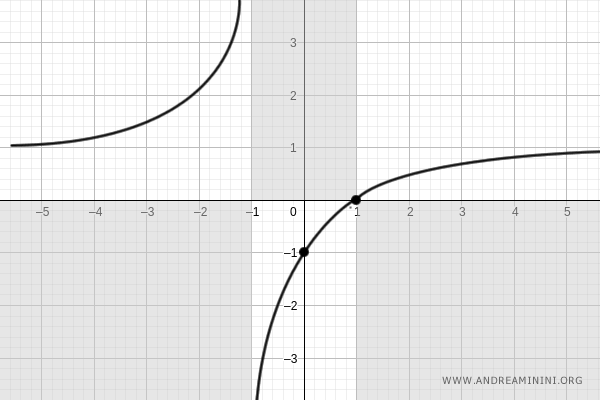
final graph of the function

And so on.