Injective Functions
What Is an Injective Function?
A mathematical function $f(x)$ is said to be injective if distinct elements in the domain correspond to distinct images in the codomain: $$ \text{if } x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$ and if two inputs are equal, their images must also be equal: $$ \text{if } x_1 = x_2 \Rightarrow f(x_1) = f(x_2) $$
Venn diagrams help visualize this concept more intuitively.

Alternatively, a function from A to B is injective if every element in A maps to a unique element in B.
Here, set A is the domain of the function $f(x)$, and set B is the codomain.
Note. The formal mathematical definition of an injective function is: $$ \forall x_1, x_2 \in D_f \mid x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$ That is, for any pair of distinct values $x_1$ and $x_2$ in the domain $D_f$, the outputs must be different: $f(x_1) \ne f(x_2)$.
It’s important to note that the target set B doesn’t necessarily coincide with the codomain. Some elements in B might not be images of any element in A.
In such cases, the actual codomain (C) of the function may be a proper subset of B.

A Practical Example
Example 1
The following function, defined over the set of real numbers ℝ, is injective:
$$ f(x) = x + 1 $$
This is because for every $x \in \mathbb{R}$, the output $f(x)$ is unique and differs from the output corresponding to any other input.
| x | y = f(x) |
|---|---|
| -3 | -2 |
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
Each input $x$ in the domain produces a distinct output $y = f(x)$.

Note. From a graphical standpoint, a function is injective if any horizontal line intersects its graph at most once. That is, it either touches the graph at a single point or not at all.
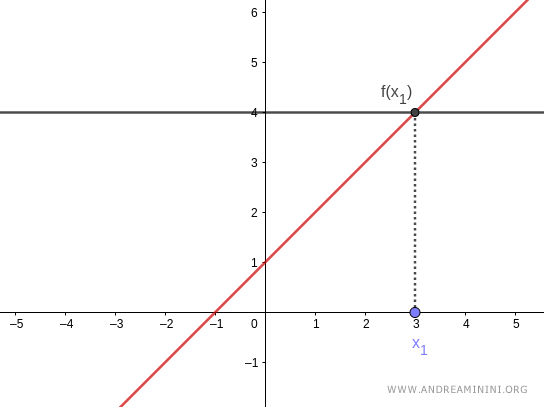
This reflects the idea that every $x$ in the domain maps to one and only one distinct $y$ in the codomain.
Example 2
The following function is not injective:
$$ f(x) = x^2 $$
In this case, different inputs can yield the same output.
| x | y = f(x) |
|---|---|
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
For instance, $f(-2) = f(2) = 4$, so the function fails the injectivity test.
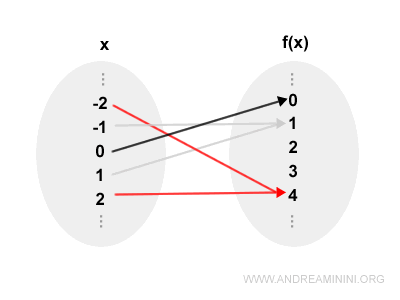
Note. Graphically, a function is not injective if there exists at least one horizontal line that intersects its graph at more than one point. This means there are two or more distinct inputs that map to the same output value.

And so on.
