Discontinuous Function

A function f(x) is said to be discontinuous at a point x₀ if the limit of f(x) as x approaches x₀ is not equal to the value of the function at that point. $$ \lim_{x \rightarrow x_0} f(x) \ne f(x_0) $$ The point x₀ is called a point of discontinuity.

Example of a discontinuous function

Removable vs. non-removable discontinuities

• A discontinuity is called removable if it can be eliminated by appropriately redefining the function to make it continuous.
• It is called non-removable if it cannot be eliminated in this way.

What causes discontinuities?

Discontinuities can arise for several reasons:

Jump Discontinuity (First Kind)

At x₀, the right-hand limit and left-hand limit of the function are not equal. This is known as a jump discontinuity or discontinuity of the first kind. $$ \lim_{x \rightarrow x_0^+} f(x) \ne \lim_{x \rightarrow x_0^-} f(x) $$

The function may or may not be defined at x₀.

Example

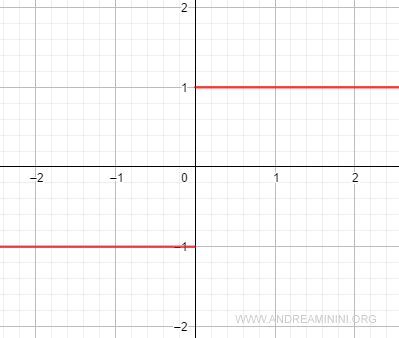
The sign function has a discontinuity at x₀ = 0:

$$ \frac{|x|}{x} $$

because the right-hand and left-hand limits differ:

$$ \lim_{x \rightarrow 0^+} \frac{|x|}{x} = 1 $$

$$ \lim_{x \rightarrow 0^-} \frac{|x|}{x} = -1 $$

Here is the graph:

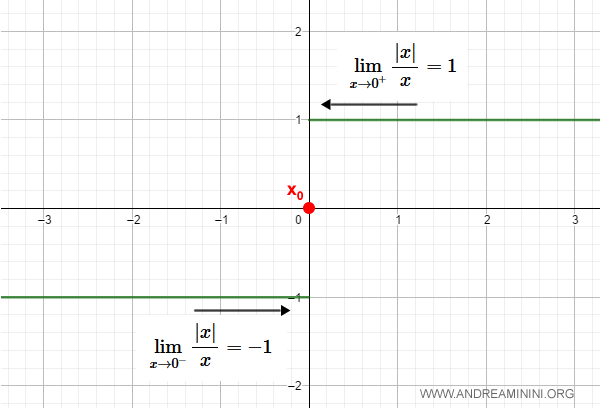
At x₀, the function jumps from -1 to +1.

Essential Discontinuity (Second Kind)

At x₀, one or both of the one-sided limits is infinite or does not exist. This is called an essential discontinuity or discontinuity of the second kind.
$$ \lim_{x \rightarrow x_0^±} f(x) \ne f(x_0) = \{ ±\infty , \text{does not exist} \} $$

Example

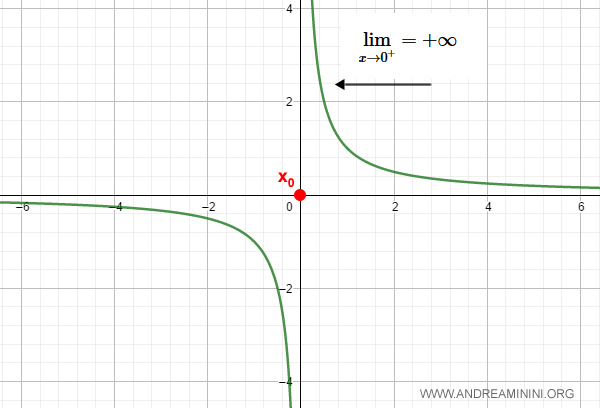
The function $$ \frac{1}{x} $$ is discontinuous at x₀ = 0,

because the right-hand limit tends to infinity:

$$ \lim_{x \rightarrow 0^+} = +\infty $$

Note. In this case, the left-hand limit tends to negative infinity: $$ \lim_{x \rightarrow 0^-} = -\infty $$ In general, a discontinuity of the second kind occurs if at least one of the one-sided limits is infinite (±\infty).

Here is the graph:

Removable Discontinuity (Third Kind)

At x₀, the limit of the function exists but does not equal the function value at that point: $$ \lim_{x \rightarrow x_0} f(x) \ne f(x_0) $$

This is known as a removable discontinuity because the discontinuity can be eliminated by redefining the function value at x₀ to match the limit.

This type of discontinuity often occurs in piecewise-defined functions.

Example

Consider the function:

$$ f(x) = \frac{\sin x}{x} $$

At x₀ = 0, the function is undefined, but the limit exists:

$$ \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1 $$

This is a well-known limit.

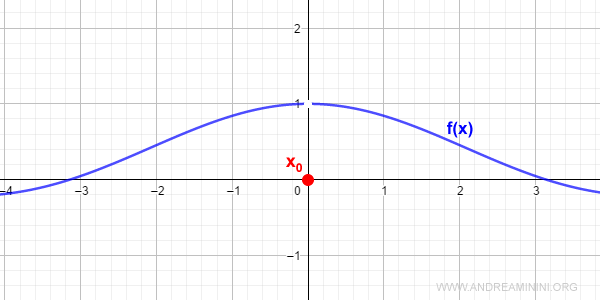
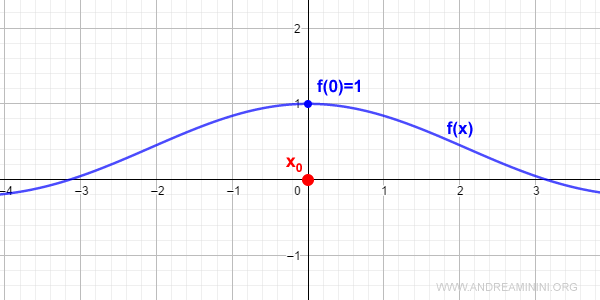
We can eliminate the discontinuity by defining f(0) = 1:

$$ f(x) = \begin{cases} \frac{\sin x}{x} \: \text{if} \: x \ne 0 \\ 1 \: \text{if} \: x = 0 \end{cases} $$

This redefinition makes the function continuous:

Example 2

Now consider this piecewise function:

$$ f(x) = \begin{cases} x+2 \: \text{if} \: x \ne 2 \\ 1 \: \text{if} \: x = 2 \end{cases} $$

This function has a point of discontinuity at x₀ = 2.

The limit as x approaches 2 exists:

$$ \lim_{x \rightarrow 2} f(x) = 4 $$

In other words, both the left-hand and right-hand limits are equal.

However, the function value at x = 2 is:

$$ f(2) = 1 $$

So the limit exists at x₀, but the function takes on a different value.

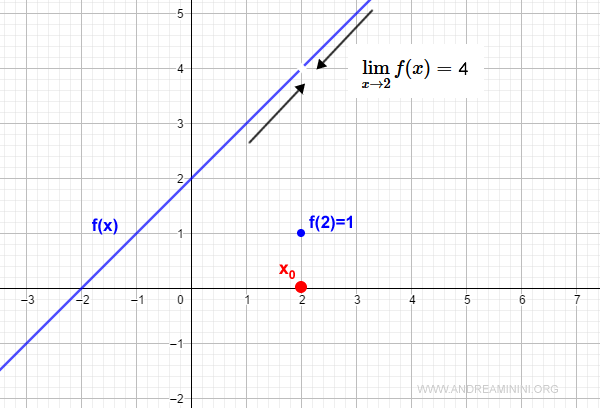
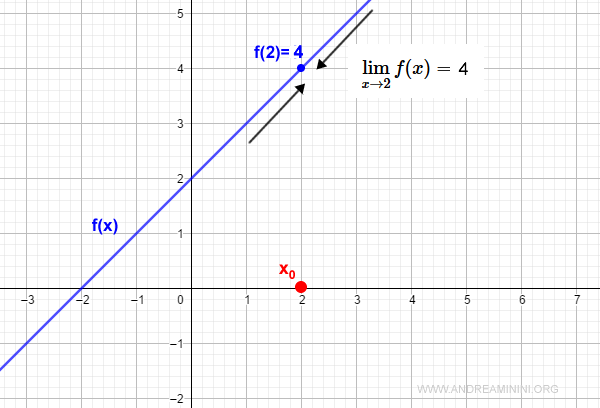
To eliminate this discontinuity, we simply redefine the function as:

$$ f(x) = \begin{cases} x+2 \: \text{if} \: x \ne 2 \\ 4 \: \text{if} \: x = 2 \end{cases} $$

This removes the discontinuity:

And so on.