Isolated points of a set
Let \( x_0 \) be a real number belonging to a subset \( A \subset \mathbb{R} \). The point \( x_0 \) is said to be an isolated point of the set \( A \) if there exists at least one neighborhood of \( x_0 \) that contains no elements of \( A \) other than \( x_0 \) itself.
Intuitively, this means that around \( x_0 \) it is possible to select an interval small enough to intersect the set \( A \) only at the point \( x_0 \).
A neighborhood of \( x_0 \) is an open interval of the form
\[ I = (x_0 - r,\; x_0 + r) \]
where \( r > 0 \) is a positive real number.
The point \( x_0 \) is isolated if there exists at least one value of \( r \) such that
\[ I \cap A = \{x_0\} \]
This condition does not need to hold for every neighborhood of \( x_0 \). The existence of a single neighborhood with this property is sufficient.
How to determine whether a point is isolated
To determine whether a point \( x_0 \) is isolated:
- start from a point belonging to the set \( A \);
- identify at least one neighborhood of \( x_0 \) that contains no other points of \( A \);
- if such a neighborhood exists, then the point is isolated. Conversely, if every neighborhood contains other points of the set, the point is not isolated.
A concrete example
Consider the set \( A \), defined as a sequence of rational numbers
\[ A = \left\{ 0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \dots , \frac{n}{n+1} \right\} \]
where \( n \) is an arbitrary natural number.
We represent this set on the real line and focus on the point \( 0 \).
It is possible to find a neighborhood of \( 0 \) that contains no other elements of \( A \), for example \( \left(-\frac{1}{3}, \frac{1}{3}\right) \).
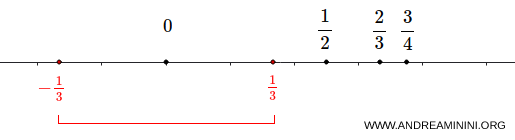
Therefore, \( 0 \) is an isolated point of the set \( A \).
By the same reasoning, and by choosing sufficiently small neighborhoods, one can show that every element of the set \( A \) is an isolated point.
Notes
Some remarks and additional observations concerning isolated points
- Finite sets
If a set contains only finitely many points, then all of its points are isolated. For example \[ B = \{-1,\; 0,\; \tfrac{3}{5},\; 6\} \] This set consists of four distinct points. For each of them, one can construct a neighborhood that is sufficiently small to exclude all the others. - Infinite sets consisting exclusively of isolated points
A set may be infinite and yet consist entirely of isolated points. For instance, the set of natural numbers is infinite, and every natural number is an isolated point \[ \mathbb{N} = \{0,1,2,3,\dots\} \] For each natural number \( n \), it suffices to consider a neighborhood of radius \( \tfrac{1}{2} \), which contains no other natural numbers. \[ (n-\tfrac{1}{2},\; n+\tfrac{1}{2}) \] As a consequence, all natural numbers are isolated points. - An isolated point is never an accumulation point
By definition, there always exists a region around an isolated point in which the set contains no other elements. This distinction is fundamental in the study of limits of functions and in the analysis of the local structure of subsets of the real line.
And so on.
