Translations of a graph

A translation of a graph is a geometric transformation that changes the position of a graph while preserving its shape.

More precisely, a translation consists of a rigid displacement of the graph of a function in the Cartesian plane.

The adjective "rigid" indicates that no deformation occurs: the graph retains both its geometric shape and its curvature.

A translation may take place in several ways: along the x-axis, along the y-axis, or simultaneously along both axes.

What is it used for? Translations are commonly used to visualize how a function responds to changes in its parameters, and they often serve as a first step in the study of more advanced transformations such as dilations and reflections. An important applied context is telecommunications, where horizontal translations are used to model the time delay of a signal.

Horizontal translation
Vertical translation
Combined translation

Horizontal translation

Starting from a generic function $ y = f(x) $, a horizontal translation by $ a $ units is obtained by modifying the argument of the function:

$ y = f(x - a) $ produces a translation of the graph to the right by $ a $ units.
$ y = f(x + a) $ produces a translation of the graph to the left by $ a $ units.

It is worth noting that shifting the graph "forward", meaning to the right, involves a sign that may appear counterintuitive. The minus sign ( $ -a $ ) translates the graph to the right, whereas the plus sign ( $ +a $ ) translates it to the left.

Practical example

Consider the function $ f(x) = x^2 $.

graph of the function y equals x squared

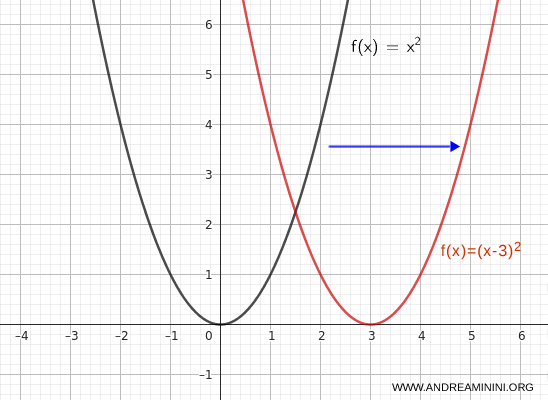
Translate the graph of the function to the right.

$$ y = (x - 3)^2 $$

In this case, the vertex of the parabola shifts from $ (0, 0) $ to $ (3, 0) $.

horizontal translation of a parabola to the right

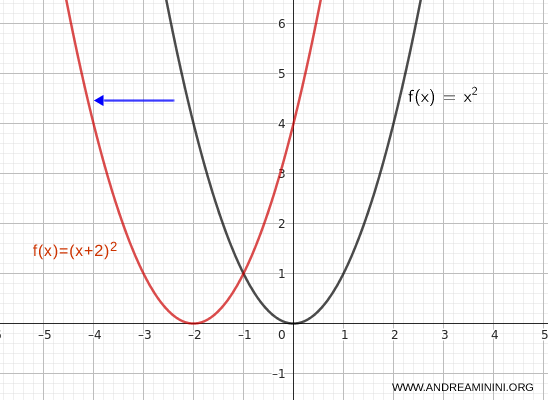
Now translate the graph of the function to the left.

$$ y = (x + 2)^2 $$

Here, the vertex moves from $ (0, 0) $ to $ (-2, 0) $.

horizontal translation of a parabola to the left

Vertical translation

Starting from a function $ y = f(x) $, a vertical translation by $ b $ units is obtained by adding or subtracting a constant term outside the function.

$ y = f(x) + b $ translates the graph upward by $ b $ units.
$ y = f(x) - b $ translates the graph downward by $ b $ units.

In this case, the sign behaves as expected: the plus sign (+b) shifts the graph upward, while the minus sign (-b) shifts it downward.

Practical example

Consider again the function from the previous example.

$$ f(x) = x^2 $$

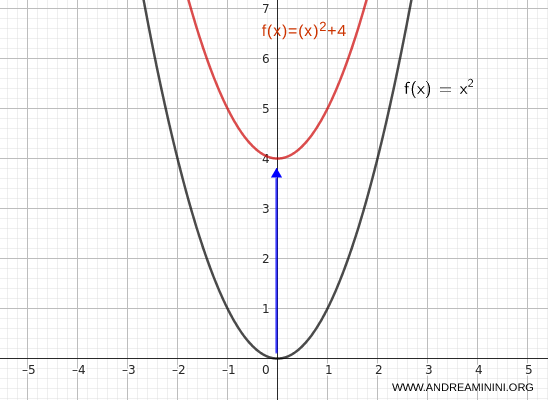
To translate the graph upward by 4 units, write:

$$ y = x^2 + 4 $$

With this transformation, the vertex of the parabola moves from $ (0, 0) $ to $ (0, 4) $.

vertical translation of a parabola upward

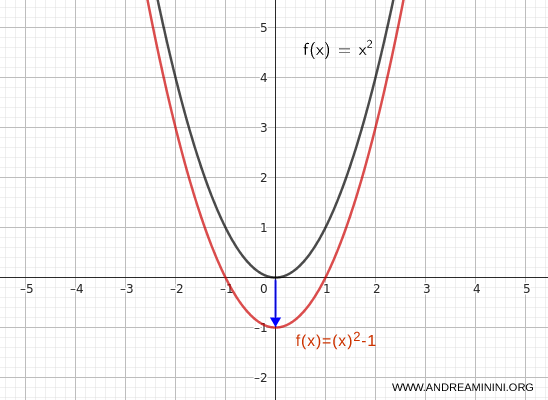
If instead the graph is translated downward by 1 unit, write:

$$ y = x^2 - 1 $$

In this case, the vertex becomes $ (0, -1) $.

vertical translation of a parabola downward

Combined translation

A combined translation is a transformation that applies a horizontal translation and a vertical translation simultaneously.

$ y = f(x - a) + b $ translates the graph by $ a $ units to the right and by $ b $ units upward.
$ y = f(x + a) - b $ translates the graph by $ a $ units to the left and by $ b $ units downward.

Example

Once again, consider the function

$$ f(x) = x^2 $$

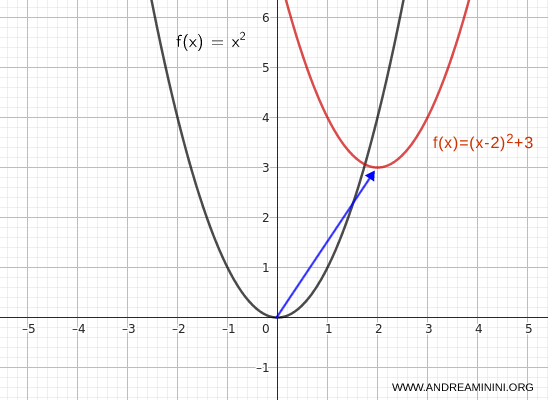
To translate the graph 2 units to the right and 3 units upward, write:

$$ y = (x - 2)^2 + 3 $$

As a result of the combined horizontal and vertical translations, the vertex of the parabola moves from $ (0, 0) $ to $ (2, 3) $.

combined horizontal and vertical translation of a parabola

As another example, to translate the graph 1 unit to the left and 2 units downward, write:

$$ y = (x + 1)^2 - 2 $$

In this case, the vertex of the parabola moves from $ (0, 0) $ to the point $ (-1, -2) $.

another example of a combined translation of a parabola

And so on.