Maximum and Minimum of a Function

The maximum and minimum of a function are points within an interval $ x \in [a, b] $ at which the function $ y = f(x) $ attains its greatest and least values, respectively.

These extrema may be either absolute or relative:

Absolute maximum or minimum: The point at which $ f(x) $ achieves its largest or smallest value over the entire interval $ [a, b] $.
Relative (local) maximum or minimum: A point where $ f(x) $ achieves a largest or smallest value within some neighborhood of $ x_0 $.

Example

example of absolute and relative maximum and minimum

At $ x_1 $, the function $ f(x) $ attains an absolute maximum on $ [a, b] $, and at $ x_2 $ it attains an absolute minimum.

At $ x_3 $ and $ x_4 $, the function has only a relative (local) maximum and minimum, respectively.

Note: An absolute maximum (or minimum) on $ [a, b] $ is, by definition, also a relative maximum (or minimum) in any neighborhood of that point. Thus, $ x_1 $ is both an absolute and a relative maximum, while $ x_2 $ is both an absolute and a relative minimum.

Relative Maximum and Minimum

Consider a point $$ x_0 $$, and examine all points within a neighborhood of radius $ \delta $ about $ x_0 $:

$$ |x - x_0| < \delta $$

If $ f(x_0) $ exceeds all nearby values of $ f(x) $, then $ x_0 $ is a relative maximum:

$$ f(x_0) > f(x) $$

For example:

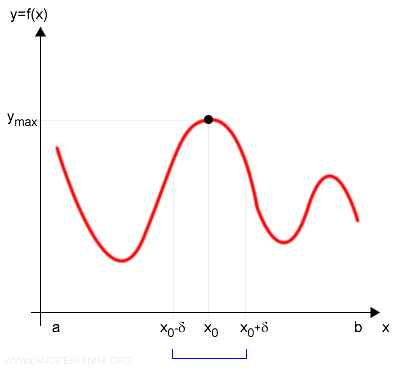
example of a relative maximum

Conversely, if $ f(x_0) $ is smaller than all nearby values of $ f(x) $, then $ x_0 $ is a relative minimum:

$$ f(x_0) < f(x) $$

For example:

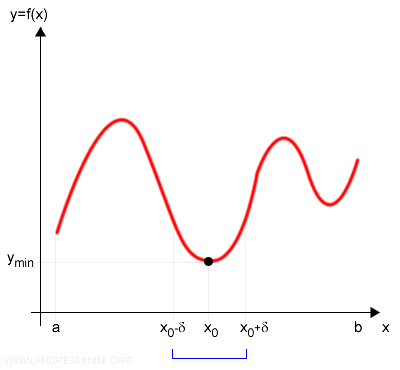
example of a relative minimum

Note: For relative extrema, the inequality (greater than or less than) holds only within some neighborhood of $x_0 $. It need not hold over the entire interval $ [a, b] $ where the function is defined.

And so on.