Lipschitz Functions

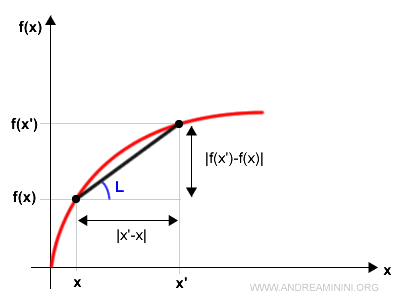
A function f(x) is said to be Lipschitz continuous on an interval I ⊆ ℝ if there exists a constant L such that $$ |f(x) - f(x')| \le L |x - x'| $$ for all x, x′ in I.

In such functions, the rate of change in the output is bounded by a constant L, known as the Lipschitz constant.

This condition is stronger than mere continuity.

What does this mean? Geometrically, it means that for any two points in the interval, the slope of the secant line connecting them is always less than or equal to L.

The concept was introduced by the German mathematician Rudolph Otto Sigismund Lipschitz.

How to Identify Lipschitz Functions

If f(x) is differentiable on an interval I, then it is Lipschitz continuous on I with constant L if and only if the absolute value of its derivative is bounded by L for all x in I: $$ |f'(x)| \le L \quad \forall x \in I $$

In other words, any differentiable function whose derivative remains bounded over the interval is Lipschitz continuous.

Proof

Suppose that for every x in I, $$ |f'(x)| \le L $$

Applying the Mean Value Theorem on [x, x′] gives:

$$ |f(x) - f(x')| = |f'(x_0)(x - x')| \le L \cdot |x - x'| $$

This confirms the Lipschitz condition.

Now let x′ = x + h:

$$ |f(x) - f(x + h)| \le L |h| $$

Which implies, reversing the order:

$$ |f(x + h) - f(x)| \le L |h| $$

Dividing both sides by |h|:

$$ \frac{|f(x + h) - f(x)|}{|h|} \le L $$

Taking the limit as h → 0 yields the derivative:

$$ \lim_{h \to 0} \frac{|f(x + h) - f(x)|}{|h|} = |f'(x)| \le L $$

Note. The Lipschitz condition $$ |f(x) - f(x_0)| \le L |x - x_0| $$ can also be expressed as $$ \frac{|f(x) - f(x_0)|}{|x - x_0|} \le L $$ This is the difference quotient, which geometrically corresponds to the slope of the secant line between two points.

Taking the limit as h → 0 gives the derivative at x₀: $$ f'(x_0) = \lim_{h \to 0} \frac{|f(x_0 + h) - f(x_0)|}{|h|} \le L $$ Therefore, if the derivative is bounded across the entire interval I, the function is Lipschitz continuous.

Examples

_{Example 1}

The function f(x) = x² is Lipschitz continuous on the interval [0, 4] with L = 8.

$$ f(x) = x^2 $$

Since f is differentiable, we compute its derivative:

$$ f'(x) = 2x $$

We then evaluate the change in slope between x₀ = 0 and x₁ = 4:

$$ |f'(x_1) - f'(x_0)| = |2(4) - 2(0)| = 8 $$

Hence, the derivative is bounded by 8 over [0, 4]:

$$ \frac{|f'(x_1) - f'(x_0)|}{|x_1 - x_0|} \le 8 $$

The graph below illustrates this:

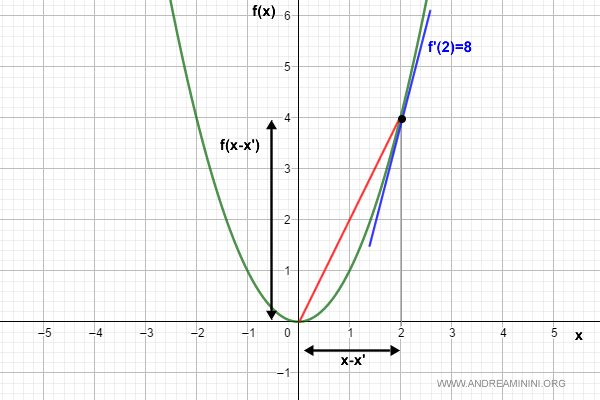
Throughout [0, 2], all tangent lines to the curve have slope less than 8.

Therefore, f(x) = x² is Lipschitz continuous on [0, 4] with Lipschitz constant L = 8.

Example 2

The sine function is Lipschitz continuous on ℝ with L = 1:

$$ f(x) = \sin x \quad \Rightarrow \quad f'(x) = \cos x $$

Since |cos x| ≤ 1 for all x ∈ ℝ, the function satisfies the Lipschitz condition globally with L = 1.

Lipschitz Continuity Implies Uniform Continuity

Every Lipschitz continuous function is also uniformly continuous on its domain.

Given any ε > 0, choose δ = ε/L.

Then:

$$ \epsilon > 0 \quad \Rightarrow \quad \delta = \frac{\epsilon}{L} $$

So for any x, x′ in I such that |x - x′| < δ, we have:

$$ |f(x) - f(x')| < L |x - x'| < \epsilon $$

Thus, the condition for uniform continuity is automatically fulfilled.

Caution. The converse does not hold: a uniformly continuous function is not necessarily Lipschitz continuous.

Counterexample

The function f(x) = √x is uniformly continuous on [0, 1], but not Lipschitz continuous there.

As x → 0, the derivative $$ f'(x) = \frac{1}{2\sqrt{x}} $$ tends to infinity.

Therefore, no constant L satisfies the Lipschitz condition on [0, 1].

Note. However, the same function is Lipschitz continuous on [1, ∞), where the growth can be bounded by a suitable constant L.

And so on.