Continuous Functions

A function f(x) is said to be continuous at a point x₀ if the limit of the function as x approaches x₀ is equal to f(x₀): $$ \lim_{x \rightarrow x_0} f(x) = f(x_0) $$

The graph of a continuous function is a smooth, unbroken curve with no gaps or interruptions.

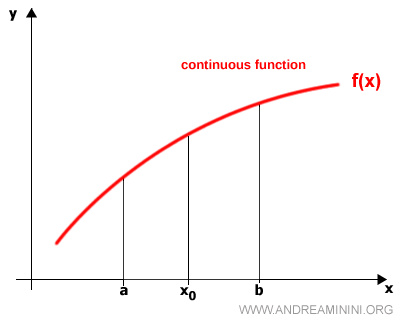
Continuity on an Interval

A function is continuous on the interval [a, b] if it is continuous at every point within the interval:

$$ \lim_{x \rightarrow x_0} f(x) = f(x_0) \ \ \forall \ x_0 \in [a, b] $$

At the endpoints of the interval, one-sided limits are considered: the right-hand limit at the left endpoint a:

$$ \lim_{x \rightarrow a^+} f(x) = f(a) $$

and the left-hand limit at the right endpoint b:

$$ \lim_{x \rightarrow b^-} f(x) = f(b) $$

A Practical Example

Consider the function:

$$ f(x) = x^2 $$

Let us check whether the function is continuous at x₀ = 2:

$$ \lim_{x \rightarrow 2} x^2 = 4 $$

At x₀ = 2, the value of the function is:

$$ f(2) = 4 $$

Since the limit matches the function value:

$$ \lim_{x \rightarrow 2} x^2 = f(2) $$

we can conclude that the function x² is continuous at x₀ = 2.

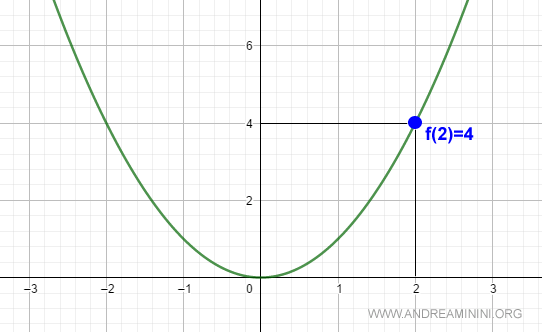
The same conclusion holds for any other point x in the domain (−∞, ∞) of the function.

And so on.