Bounded and Unbounded Functions

What is a bounded function?

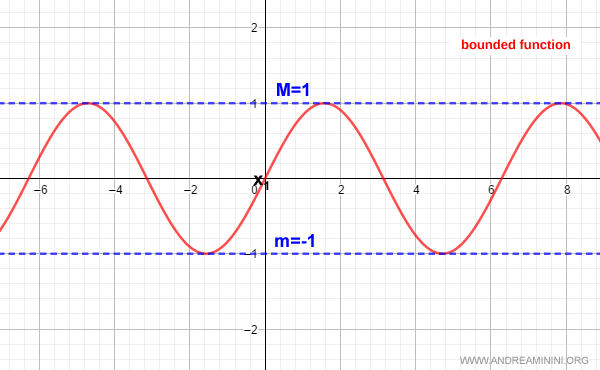
A bounded function is one whose values $f(x)$ remain confined between a minimum and a maximum.

Geometrically, the graph of a bounded function lies entirely between two horizontal lines (parallel to the x-axis).

In such a function, the range of values is restricted between two real numbers:

• Minimum: the smallest value attained by $f(x)$ on an interval $[a, b]$
• Maximum: the largest value attained by $f(x)$ on an interval $[a, b]$

If it is not possible to find two real numbers that bound the range of the function, the function is said to be unbounded.

Example of an unbounded function: The function $f(x) = x^3$ is unbounded - it has neither a finite minimum nor maximum.

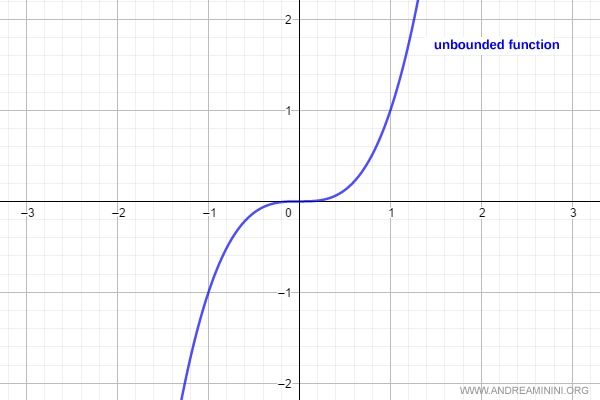
A function is considered bounded if it is bounded both above and below.

A Practical Example

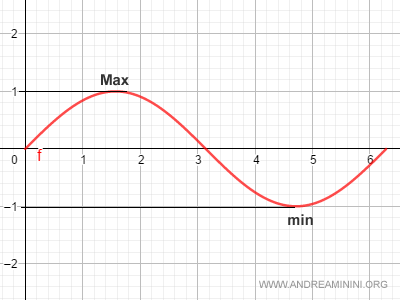
Let’s consider the sine function:

$$ f(x) = \sin(x) $$

The domain of this function is the set of real numbers:

$$ \text{Dom}(f) = \mathbb{R} $$

Its range consists of infinitely many values contained within the closed interval $[-1, 1]$:

$$ \text{Im}(f) = [-1, 1] $$

The range is thus bounded both above and below.

The function $f(x)$ has both a maximum and a minimum:

$$ M = 1 $$

$$ m = -1 $$

Therefore, the sine function is bounded on its entire domain.

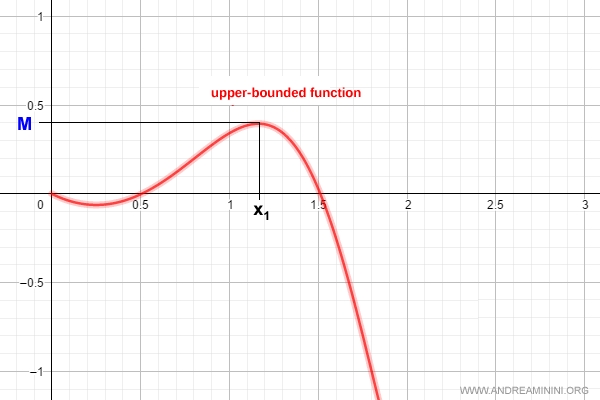
Upper-Bounded Functions

A function $f(x)$ defined on an interval $(a, b)$ is upper-bounded if at least one of the following conditions holds:

1. There exists a real number $M$ such that $f(x) \le M$ for all $x \in (a, b)$.
2. The range of $f(x)$ is bounded above.
3. The supremum of the range is finite: $$ \sup(\text{Im}(f)) < +\infty $$

If none of these conditions hold, the function is said to be unbounded above.

Example: An upper-bounded function - $f(x)$ has a finite maximum value $M$.

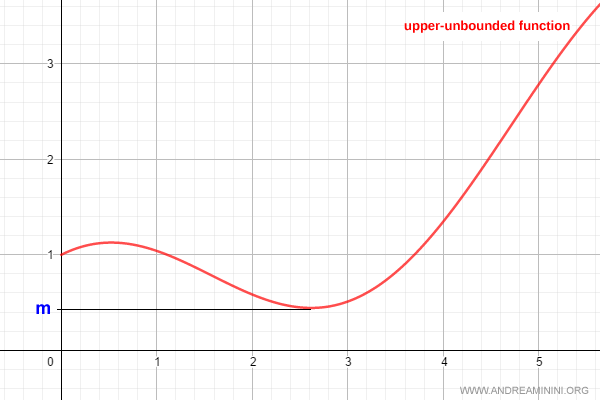
Upper-Unbounded Functions

A function $f(x)$ defined on $(a, b)$ is upper-unbounded on its domain if at least one of the following conditions holds:

1. For every $M > 0$, there exists $x \in (a, b)$ such that $f(x) > M$.
2. The range of $f(x)$ is unbounded above.
3. The supremum of the range is infinite: $$ \sup(\text{Im}(f)) = +\infty $$

Example: An upper-unbounded function.

Lower-Bounded Functions

A function $f(x)$ defined on an interval $(a, b)$ is lower-bounded if at least one of the following conditions holds:

1. There exists a real number $m$ such that $f(x) \ge m$ for all $x \in (a, b)$.
2. The range of $f(x)$ is bounded below.
3. The infimum of the range is finite: $$ \inf(\text{Im}(f)) > -\infty $$

If none of these conditions hold, the function is said to be unbounded below.

Example: A lower-bounded function - $f(x)$ attains a minimum value $m$.

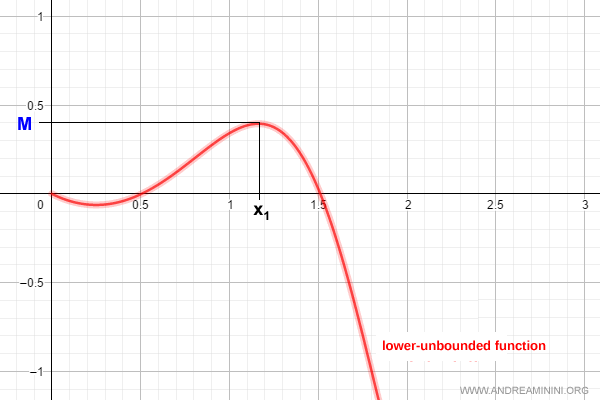
Lower-Unbounded Functions

A function $f(x)$ defined on $(a, b)$ is lower-unbounded on its domain if at least one of the following conditions holds:

1. For every $m \in \mathbb{R}$, there exists $x \in (a, b)$ such that $f(x) < m$.
2. The range of $f(x)$ is unbounded below.
3. The infimum of the range is infinite: $$ \inf(\text{Im}(f)) = -\infty $$

Example: A lower-unbounded function.

And so on.