Monotonic Functions

What Is a Monotonic Function?

A function f(x) is said to be monotonic on an interval [a, b] if, for any two values x₁ and x₂ in that interval such that x₂ > x₁, the following holds:

• Increasing $$ f(x_1) \le f(x_2) $$
• Strictly increasing $$ f(x_1) < f(x_2) $$
• Decreasing $$ f(x_1) \ge f(x_2) $$
• Strictly decreasing $$ f(x_1) > f(x_2) $$

Examples

Example 1

This function is monotonically increasing.

However, it's not strictly increasing since it remains constant over some intervals.

In technical terms, it is a non-decreasing function.

Example 2

This function is strictly increasing as it consistently rises and never flattens out.

Example 3

This function is monotonically decreasing.

It's not strictly decreasing because there are segments where the function remains constant.

Therefore, it is classified as a non-increasing function.

Example 4

This function is strictly decreasing since it continuously decreases without ever staying constant.

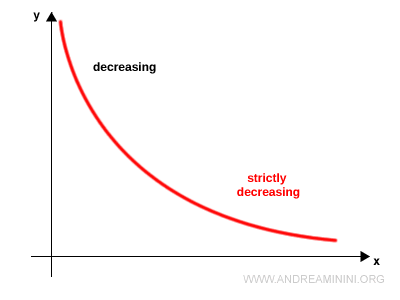
Strictly Monotonic Functions

A function is strictly monotonic if it is either strictly increasing or strictly decreasing throughout its domain.

In simpler terms, strictly monotonic functions never have flat intervals - they either always increase or always decrease.

Key Properties of Strictly Monotonic Functions

Strict monotonicity plays a central role in mathematical analysis, as it ensures the function is invertible.

Every strictly monotonic function is invertible, meaning it always has an inverse function.

Example

The function f(x) = x + 1 is strictly increasing:

$$ f(x)=x+1 $$

As such, it is also invertible, and its inverse is:

$$ f^{-1}(y)=y-1 $$

This principle applies broadly to all strictly monotonic functions.