Asymptotes

Definition of an asymptote

In mathematics, an asymptote is a line or curve that a function’s graph approaches arbitrarily closely as the independent variable x tends to plus or minus infinity, or approaches a specific finite value.

More precisely, a line qualifies as an asymptote if the distance between the graph of the function and the line tends to 0 as the independent variable  x tends to infinity or to a finite limit.

Equivalently, the graph progressively converges toward the line, becoming arbitrarily close to it.

• If the asymptote is a straight line, it is referred to as a linear asymptote.
• If the asymptote is a curve, it is referred to as a curvilinear asymptote.

In mathematical analysis, three principal categories of asymptotes are identified when studying a function f(x): horizontal, vertical, and oblique.

Horizontal Asymptotes

A horizontal asymptote is determined by evaluating the limit of the function as x approaches positive or negative infinity:

$$ \lim_{x \rightarrow ±∞ } f(x) = c $$

A horizontal asymptote exists if this limit equals a finite real number.

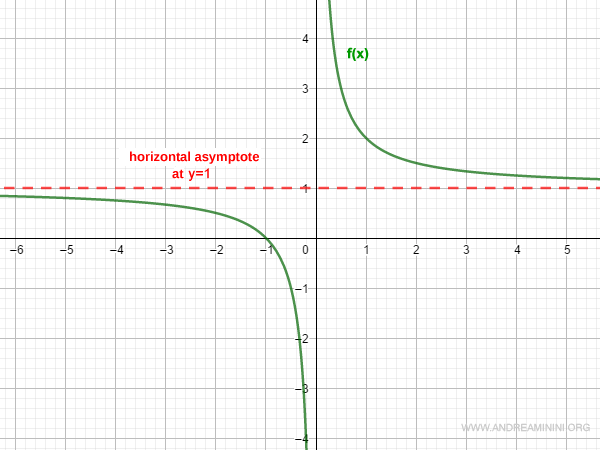
Here’s a simple example of a horizontal asymptote:

In practice, the horizontal asymptote is a line that runs parallel to, or coincides with, the x-axis.

Note that the horizontal asymptotes as x → +∞ and x → -∞ do not necessarily have to be the same.

Example

Let’s determine the horizontal asymptotes of the function:

$$ f(x) = \frac{x+1}{x} $$

First, we compute the limit as x → +∞:

$$ \lim_{x \rightarrow +∞ }\frac{x+1}{x} = 1 $$

Therefore, the function has a horizontal asymptote at y = 1 as x → +∞.

Note. This is an indeterminate form ∞/∞, which can easily be resolved using L'Hôpital’s Rule.

Now, we compute the limit as x → -∞:

$$ \lim_{x \rightarrow -∞ }\frac{x+1}{x} = 1 $$

Thus, the function also has a horizontal asymptote at y = 1 as x → -∞.

 

Vertical Asymptotes

A vertical asymptote occurs at points where the function is undefined. It is determined by evaluating the limit of f(x) as x approaches x₀ from the right and from the left: $$ \lim_{x \rightarrow x_0^+ } f(x) = ±∞ $$ $$ \lim_{x \rightarrow x_0^- } f(x) = ±∞ $$ where x₀ is a point of discontinuity.

A vertical asymptote exists at x₀ if these limits tend to positive or negative infinity.

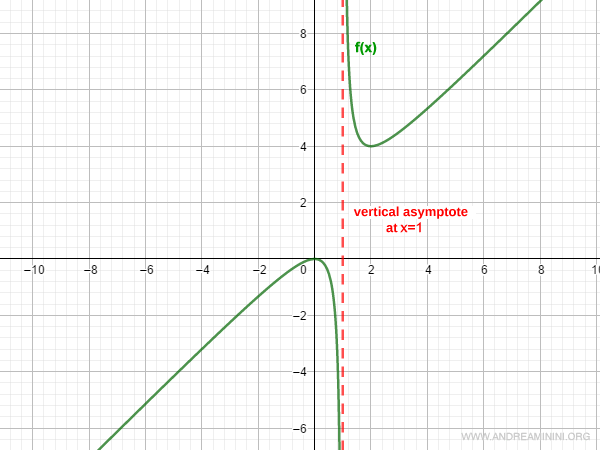
Here’s a practical example of a vertical asymptote:

In practice, a vertical asymptote is a line parallel to, or coinciding with, the y-axis.

Example

Let’s check whether the following function has any vertical asymptotes:

$$ f(x) = \frac{x^2}{x-1} $$

This function is undefined at x = 1.

We now evaluate the limit as x approaches 1 from both sides:

$$ \lim_{x \rightarrow 1^+ } \frac{x^2}{x-1} = +∞ $$

$$ \lim_{x \rightarrow 1^- } \frac{x^2}{x-1} = -∞ $$

Therefore, the function has a vertical asymptote at x = 1.

Oblique Asymptotes

A function has an oblique asymptote if the limit, as x approaches +∞ or -∞, of the difference between the function $ f(x) $ and the line $ y = mx + q $ is zero: $$ \lim_{x \rightarrow \pm \infty} \left[ f(x) - (mx + q) \right] = 0 $$ If the graph of the function admits an oblique asymptote with equation $ y = mx + q $, then the slope $ m \ne 0 $ and the intercept $ q $ are finite, and can be computed as: $$ m = \lim_{x \to \infty} \frac{f(x)}{x} $$ $$ q = \lim_{x \to \infty} \left[ f(x) - mx \right] $$

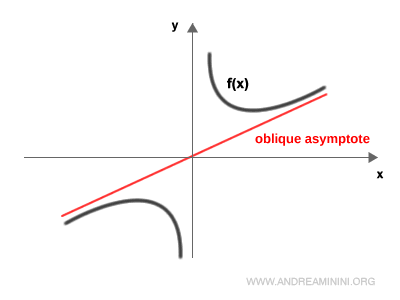
Here’s a practical example of an oblique asymptote:

To determine whether an oblique asymptote exists as x → +∞, we first calculate the slope m:

$$ m = \lim_{x \rightarrow +∞ } \frac{f(x)}{x} \ne 0 $$

Proof. If $$ \lim_{x \rightarrow +∞ } f(x) - (mx+q) = 0 $$ then we can initially set q = 0 and compute: $$ \lim_{x \rightarrow +∞ } f(x) - mx = 0 $$ Since the limit tends to zero as x → ∞, we can safely divide by x: $$ \lim_{x \rightarrow +∞ } \frac{f(x) - mx}{x} = 0 $$ $$ \lim_{x \rightarrow +∞ } \frac{f(x)}{x} - m = 0 $$ $$ \lim_{x \rightarrow +∞ } \frac{f(x)}{x} = m $$

If the slope m exists and is non-zero, we then compute the intercept q:

$$ q= \lim_{x \rightarrow ±∞ } f(x) - mx \ne ∞ $$

Proof. If $$ \lim_{x \rightarrow +∞ } f(x) - (mx+q) = 0 $$ then: $$ \lim_{x \rightarrow +∞ } f(x) - mx - q = 0 $$ $$ \lim_{x \rightarrow +∞ } f(x) - mx = q $$

If q exists and is finite, the function has an oblique asymptote y = mx + q as x → +∞. Otherwise, it does not.

The same method applies to check for an oblique asymptote as x → -∞.

Example

Let’s check whether the following function has an oblique asymptote:

$$ f(x) = \frac{x^2}{x-1} $$

First, we verify that the limit as x → ∞ is infinite:

$$ \lim_{x \rightarrow ∞} \frac{x^2}{x-1} = ∞ $$

Note. This is an indeterminate form ∞/∞, which can easily be resolved using L'Hôpital’s Rule.

Next, we determine whether the slope m is non-zero:

$$ m = \lim_{x \rightarrow ∞} \frac{ \frac{x^2}{x-1} }{x} $$

$$ m = \lim_{x \rightarrow ∞} \frac{x^2}{x(x-1)} $$

$$ m = \lim_{x \rightarrow ∞} \frac{x}{(x-1)} = 1 $$

Since m = 1 is finite and non-zero, we now compute the intercept q:

$$ q = \lim_{x \rightarrow ∞} \frac{x^2}{x-1} - mx $$

Since m = 1:

$$ q = \lim_{x \rightarrow ∞} \frac{x^2}{x-1} - x $$

$$ q = \lim_{x \rightarrow ∞} \frac{x^2-x^2+x}{x-1} $$

$$ q = \lim_{x \rightarrow ∞} \frac{x}{x-1} = 1 $$

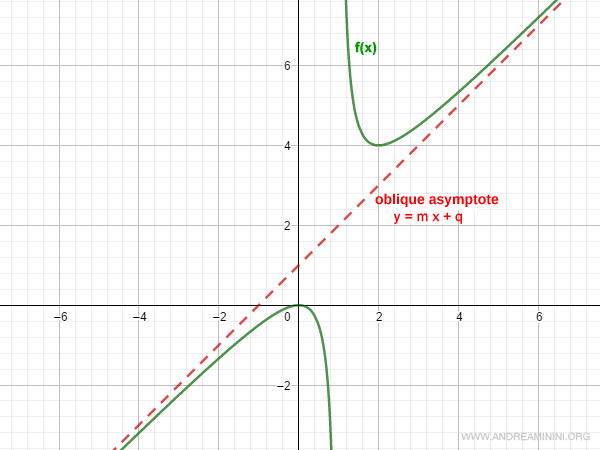
Thus, the function has an oblique asymptote with slope m = 1 and intercept q = 1:

Oblique Asymptotes of Rational Functions

A rational function $ f(x)=\frac{A(x)}{B(x)} $ admits exactly one oblique (slant) asymptote if and only if the degree $ n $ of the numerator polynomial $ A(x) $ is exactly one greater than the degree $ m $ of the denominator polynomial $ B(x) $. $$ n = m+1 $$

Example

Consider the rational function:

\[ f(x) = \frac{x^3 + 2x^2 - 1}{x^2 - 1} \]

The numerator has degree 3, while the denominator has degree 2.

$$ n=3 $$

$$ m=2 $$

The difference is $ 3-2=1 $, so an oblique asymptote exists.

To determine it, carry out polynomial division

$$ \begin{array}{cccc|cc} x^3 & +2x^2 & 0x & -1   & x^2 & -1  \\  -x^3 &  & +x &   & x +2 \\ \hline  & 2x^2 & +x & \\  & -2x^2 & & +2 \\ \hline  &  & -x & +1 \end{array} $$

Thus, the quotient is \( Q(x) = x+2 \) and the remainder is \( R(x) = -x+1 \)

The division of two polynomials can be written as

$$ \frac{A(x)}{B(x)} = Q(x) + \frac{ R(x) }{B(x)} $$

Explanation. Since $$ A(x):B(x) = Q(x) \text{ with remainder } R(x) $$ it follows that $$ A(x) = Q(x) \cdot B(x) + R(x) $$ Dividing both sides by $ B(x) $ gives $$ \frac{A(x)}{B(x)} = Q(x) + \frac{R(x)}{B(x)} $$

Substituting, we obtain

$$ \frac{x^3+2x^2-1}{x^2-1} = (x+2) + \frac{-x+1}{x^2-1} $$

As $ x \to \infty $, the remainder term tends to zero

$$ \lim_{x \to \infty} \frac{-x+1}{x^2-1} = 0 $$

Therefore, the graph of the function approaches the line $ y=x+2 $ as $ x \to \infty $.

In other words, for large values of $ x $, the function behaves like $ f(x) \approx x + 2 $.

Hence, the oblique asymptote is

$$ y = x + 2 $$

The key idea is that, asymptotically, the linear term \( x + 2 \) dominates, while the remainder becomes negligible. As a result, the graph gets arbitrarily close to the line \( y = x + 2 \).

And so on.