Accumulation Points

Consider a set I of real numbers. A point x₀ is called an accumulation point of I if, for any δ > 0, there exists at least one real number x in I such that $$ 0 \ne |x - x_0| < \delta $$.

If there’s at least one point x in the interval (x₀ - δ, x₀ + δ) belonging to I and distinct from x₀, then x₀ is an accumulation point of I.

Note. If the set I consists of a single point [a,b] where a = b, then I has no accumulation points, since there are no other points around x₀ besides x₀ = a.

The Case of Closed and Open Intervals

It’s essential to distinguish between closed and open intervals:

• In a closed interval [a, b] where a < b, every point within [a, b] is an accumulation point of the interval.
• In an open interval (a, b) where a < b, every point inside (a, b) is an accumulation point, and the endpoints a and b are also accumulation points of (a, b).

Therefore, the accumulation points of an open interval (a, b) are the same as those of the closed interval [a, b].

Infinitely Many Real Numbers in the Neighborhood

If I is a subset of the set of real numbers R, $$ I \subseteq R $$ then the point x₀ ∈ R is an accumulation point of I only if every neighborhood (x₀ - δ, x₀ + δ) contains infinitely many points of I distinct from x₀.

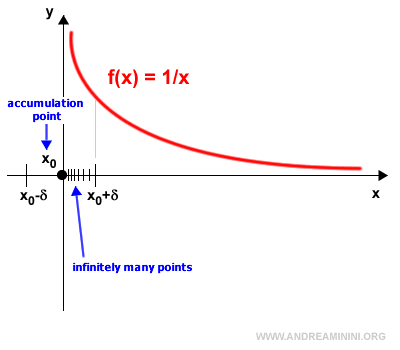
Proof

Suppose x₀ is an accumulation point. Assume, for the sake of contradiction, that there are only finitely many, say k, real numbers in the neighborhood of x₀ for some δ > 0.

$$ | x_0 - x_i | < \delta \quad \forall i = 1, \dots, k $$

Define a new δ₁ as the smallest distance between x₀ and any of these points:

$$ \delta_1 = \min | x_0 - x_i | \quad \forall i = 1, \dots, k $$

In the neighborhood (x₀ - δ₁, x₀ + δ₁), there would be no points of I other than x₀ itself.

$$ (x_0 - \delta_1, x_0 + \delta_1) $$

But this contradicts our initial assumption that x₀ is an accumulation point.

Therefore, if x₀ is an accumulation point in the real numbers R, every neighborhood around x₀ must contain infinitely many points of R.

Sequences Drawn from the Neighborhood Converge to the Accumulation Point

If x₀ is an accumulation point of a set I in R, then there exists a sequence of points x_n in I, all distinct from x₀, that converges to x₀.

Proof

Take any natural number n ∈ N to define the neighborhood radius δ:

$$ \delta = \frac{1}{n} $$

This determines a neighborhood around x₀:

$$ ( x_0 - \delta, \; x_0 + \delta ) $$

Since x₀ is an accumulation point, there are infinitely many points in I, distinct from x₀, within this neighborhood.

$$ x_0 - \frac{1}{n} < x_n < x_0 + \frac{1}{n} $$

This inequality defines three sequences taken from I for each n ∈ N.

Let’s evaluate the limits of these three sequences as n approaches infinity:

$$ \lim_{n \rightarrow \infty} \left(x_0 - \frac{1}{n}\right) < \lim_{n \rightarrow \infty} x_n < \lim_{n \rightarrow \infty} \left(x_0 + \frac{1}{n}\right) $$

The limits of the first and third sequences both converge to x₀ as n → ∞:

$$ x_0 < \lim_{n \rightarrow \infty} x_n < x_0 $$

By the Squeeze Theorem, the limit of the intermediate sequence must also converge to x₀.

This completes the proof.

Given an accumulation point x₀ of the set I, if every sequence x_n drawn from I \ {x₀} converging to x₀ results in a sequence f(x_n) converging to some limit l, then the function f(x) has a limit equal to l as x approaches x₀. $$ \lim_{x \rightarrow x_0} f(x) = l $$

Example

Consider the function f(x) = x² + 1. The point x₀ = 0 is an accumulation point relative to the set I = (-1, 0).

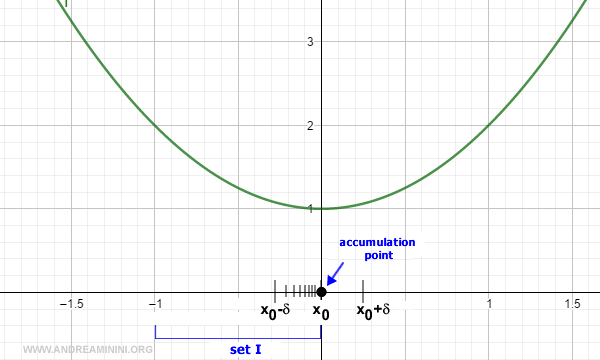
For any neighborhood (x₀ - δ, x₀ + δ), any sequence x_n drawn from I and converging to x₀ produces a sequence f(x_n) that converges to l = 1.

Hence, the limit of the function as x → 0 is 1.

$$ \lim_{x \rightarrow 0} \; x^2 + 1 = 1 $$

Infinity as an Accumulation Point

An accumulation point can also be at infinity (+∞ or -∞) for a set I ⊆ R if there’s at least one point from I in a neighborhood of infinity.

In this case, the neighborhood of the accumulation point x₀ is an interval of the form (M, +∞) that includes all real numbers x > M.

Of course, +∞ is an accumulation point only if it’s the least upper bound of the set I.

Note. The same holds for the neighborhood (-∞, -M), for any x < -M. In this case, -∞ is an accumulation point only if it’s the greatest lower bound of I.

And so on.