Right-Hand Limit
A function f(x), defined on an interval (c, d), is said to have a right-hand limit as x approaches c from the right if: $$ \lim_{x \rightarrow c^+} f(x) = l $$ In other words, for any ε > 0, there exists a δ > 0 such that whenever $$ c < x < c + δ, \text{ then } |f(x) - l| < ε. $$
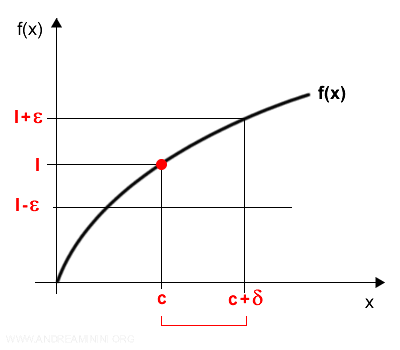
For the right-hand limit to exist, this condition must hold over the open interval (c, c + δ), which includes values strictly greater than c.
Note. When evaluating the right-hand limit of a function at a point c, we consider only values approaching c from the right. Values to the left of c - or the value of the function exactly at c - are not relevant for the right-hand limit and may or may not exist independently.
A Practical Example
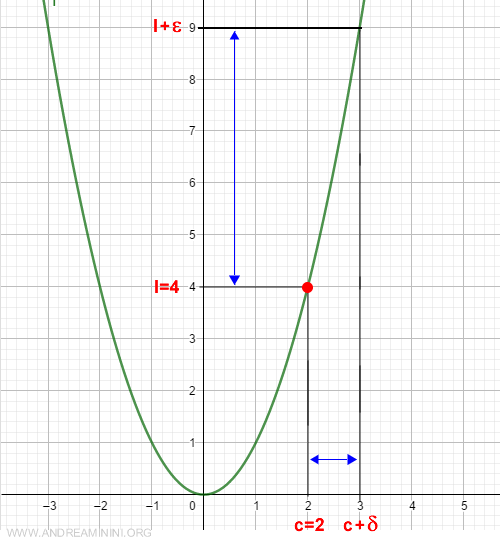
Let’s examine the function f(x) = x2 at the point c = 2.
The right-hand limit of the function is:
$$ \lim_{x \rightarrow 2^+} f(x) = 4 $$
Verification
Let’s choose an arbitrary value ε = 5, which is greater than zero.
$$ l + ε = 4 + 5 = 9 $$
This allows us to select a value δ = 1, also greater than zero, and define the interval:
$$ (c, c + δ) = (2, 2 + 1) = (2, 3) $$
For any x within the open interval (2, 3) on the x-axis, the absolute difference between f(x) and the right-hand limit l is less than ε.
Therefore, the right-hand limit of the function f(x) at x = 2 is indeed 4.
Infinite right-hand limit as x approaches x₀
Right-hand limit +∞
Let f(x) be a function defined in a right-hand neighborhood of $ x_0 $ (though not necessarily at $ x_0 $ itself). We say that f(x) tends to +∞ as x approaches $ x_0 $ from the right, and we write: \[ \lim_{x \to x_0^+} f(x) = +\infty \] if, for every positive real number $ M>0 $, one can determine a right-hand neighborhood $ I^+(x_0) $ such that: \[ f(x) > M \] for every $ x $ belonging to $ I^+(x_0) $. \[ \forall \ M > 0 \ \exists \ I^+(x_0) \ | \ f(x) > M,\ \forall \ x \in I^+(x_0) \]
In this situation, we also say that the function f diverges positively to the right of $ x_0 $.
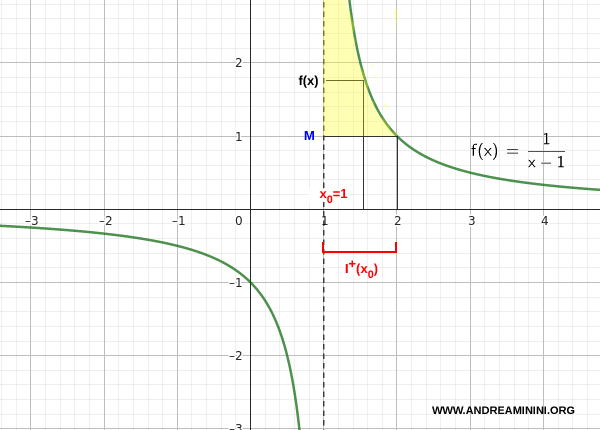
For example, consider the function
\[ f(x) = \frac{1}{x - 1} \]
We study the limit as $ x $ approaches 1 from the right.
For $ x > 1 $, the denominator is positive and tends to zero. As a consequence, f(x) grows without bound.
Therefore:
\[ \lim_{x \to 1^+} \frac{1}{x - 1} = +\infty \]
The function diverges positively to the right of 1.
Right-hand limit -∞
We say that f(x) tends to -∞ as x approaches x₀ from the right, and we write: \[ \lim_{x \to x_0^+} f(x) = -\infty \] if, for every positive real number $ M > 0 $, one can determine a right-hand neighborhood $ I^+(x_0) $ such that: \[ f(x) < -M \] for every $ x $ belonging to $ I^+(x_0) $. \[ \forall \ M > 0 \ \exists \ I^+(x_0) \ | \ f(x) < -M,\ \forall \ x \in I^+(x_0) \]
In this situation, we also say that the function f diverges negatively to the right of x₀.
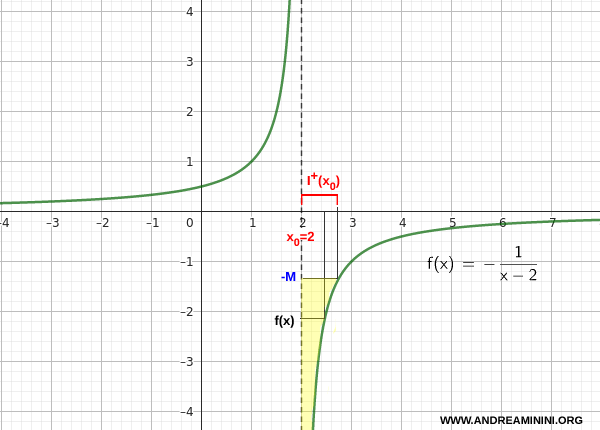
For example, consider the function
\[ f(x) = -\frac{1}{x - 2} \]
We want to study the limit as x approaches 2 from the right.
For $ x > 2 $, the denominator is positive and tends to zero, but the minus sign makes the ratio negative, with an absolute value that becomes larger and larger.
Therefore:
\[ \lim_{x \to 2^+} \left( -\frac{1}{x - 2} \right) = -\infty \]
The function diverges negatively to the right of 2.
And so on.
