Theorem on the Preservation of Sign for the Limit of a Sequence
If the limit of a sequence an as n approaches infinity converges to a value l greater than zero, then there exists some index v such that for all n > v, the terms of the sequence an remain positive. $$ \lim_{n \rightarrow \infty } a_n = l > 0 \; \rightarrow \; \exists \, v \; : \; \forall n > v, \; a_n > 0 $$
A Practical Example
Consider the sequence:
$$ a_n = \frac{n-3}{n} $$
The initial terms of this sequence are:
$$ a_1 = -2 \\ a_2 = -0.5 \\ a_3 = 0 \\ a_4 = 0.25 \\ a_5 = 0.4 \\ \vdots $$
The limit of this sequence is +1:
$$ \lim_{n \rightarrow \infty} \frac{n-3}{n} = 1 $$
According to the theorem on the preservation of sign, there exists an index v such that all terms beyond that point share the same sign as the limit, meaning an > 0 for all n > v.
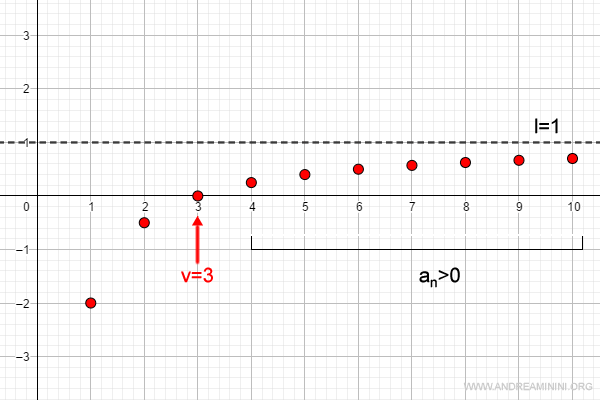
In this example, v = 3, since for all n > v, the terms of the sequence are positive, matching the sign of the limit (1).
$$ a_4 = 0.25 \\ a_5 = 0.4 \\ \vdots $$
Note. The theorem on the preservation of sign does not claim that every term in the sequence matches the sign of the limit, but only those for which n > v. In this example, the first two terms are negative, the third is zero, and only from the fourth term onward are the terms positive.
Proof
Suppose the limit l of the sequence is greater than zero (l > 0):
$$ \lim_{n \rightarrow \infty} a_n = l > 0 $$
By the definition of a limit, there exists some ε > 0 such that:
$$ | a_n - l | < \epsilon $$
Let’s choose ε = l/2:
$$ | a_n - l | < \frac{l}{2} $$
According to the theorem, there exists an index v such that for all n > v:
$$ | a_n - l | < \frac{l}{2} $$
This inequality can be rewritten as:
$$ -\frac{l}{2} < a_n - l < \frac{l}{2} $$
Adding l to all sides yields:
$$ l - \frac{l}{2} < a_n < l + \frac{l}{2} $$
Which simplifies to:
$$ \frac{l}{2} < a_n < \frac{3l}{2} $$
Focusing on the lower bound, we have:
$$ \frac{l}{2} < a_n $$
Since l > 0 by assumption, it follows that l/2 is also positive:
$$ 0 < \frac{l}{2} < a_n $$
Thus:
$$ 0 < a_n $$
This shows that all terms of the sequence beyond v are positive.
Hence, the sign of the limit persists for every n > v.
Some Useful Corollaries
Corollary 1
If all terms of a sequence are non-negative as n approaches infinity, then the limit of the sequence is also non-negative: $$ \forall n > 0 : a_n \ge 0 \; \Rightarrow \; \lim_{n \rightarrow \infty} a_n = l \ge 0 $$
The same reasoning applies in the opposite direction: if all terms of a sequence are non-positive, then the limit is also non-positive.
Proof
Suppose we have a sequence where every term is greater than or equal to zero:
$$ a_n \ge 0 \quad \forall n \ge 0 $$
Assume, for the sake of contradiction, that the limit l of the sequence is negative:
$$ \lim_{n \rightarrow \infty} a_n = l < 0 $$
Then, by the theorem on the preservation of sign, there must exist some index v > 0 such that an < 0 for all n > v:
$$ \exists \, v > 0 \; \text{ such that } \; a_n < 0 \quad \forall n > v $$
However, this is impossible because our initial assumption states that all terms of the sequence are non-negative.
Therefore, the theorem would be violated if the limit were negative.
Consequently, the limit cannot be negative and must be greater than or equal to zero.
This proves the corollary.
Corollary 2
Given two sequences an and bn converging to limits la and lb respectively, if an ≥ bn for all n > 0, then it follows that la ≥ lb. $$ \forall n > 0 \; : \; a_n \ge b_n \; \Rightarrow \; l_a \ge l_b $$
Proof
Consider two sequences an and bn converging to la and lb:
$$ l_a = \lim_{n \rightarrow \infty} a_n $$ $$ l_b = \lim_{n \rightarrow \infty} b_n $$
By assumption, every term of the sequence an is greater than or equal to the corresponding term of bn:
$$ a_n \ge b_n $$
Therefore:
$$ a_n - b_n \ge 0 $$
and consequently, the limit of their difference is also greater than or equal to zero:
$$ \lim_{n \rightarrow \infty} (a_n - b_n) \ge 0 $$
If, for the sake of contradiction, the limit of the difference an - bn were negative, then by the theorem on the preservation of sign, there would exist an index v > 0 such that an - bn < 0, implying an < bn.
This, however, contradicts our initial assumption. Hence, the theorem would not hold in such a case.
Therefore, since the limit of the difference an - bn cannot be negative, it must be greater than or equal to zero, implying la ≥ lb.
This completes the proof of the corollary.
And so on.
