Theorem on Limits of Monotonic Sequences

A monotonic sequence always possesses either a finite or an infinite limit. $$ \lim_{n \rightarrow \infty} a_n = \begin{cases} l \\ \infty \end{cases} $$ If a monotonic sequence is also bounded, then it necessarily converges to a finite limit. $$ \lim_{n \rightarrow \infty} a_n = l $$

Every monotonic sequence is also a regular sequence because it is guaranteed to have either a finite or infinite limit.

Meaning of Monotonic, Regular, and Bounded. A sequence is called monotonic if each term a_n is either always greater than or equal to, or always less than or equal to, the next term a_n+1. If the inequality is strict, the sequence is said to be strictly monotonic. A sequence is regular if it has either a finite or an infinite limit. A sequence is bounded if its terms remain confined within fixed upper and lower bounds.

Illustrative Examples

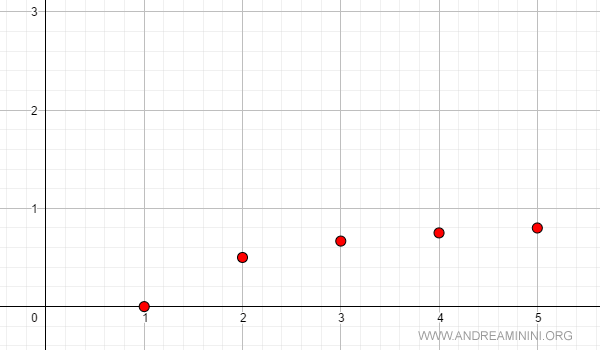
Example 1

This sequence is monotonic increasing and bounded:

$$ a_n = \frac{n-1}{n} $$

The limit of the sequence converges to 1:

$$ \lim_{n \rightarrow \infty} a_n = 1 $$

Here is its graphical representation:

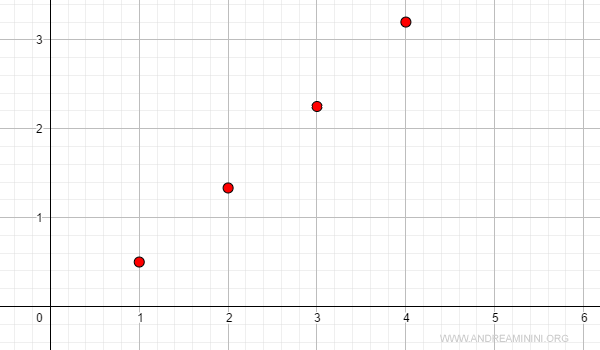
Example 2

This sequence is monotonic increasing but unbounded:

$$ a_n = \frac{n^2}{n+1} $$

The limit of the sequence is infinite:

$$ \lim_{n \rightarrow \infty} a_n = +\infty $$

Here is its graphical representation:

 

Proof

To prove this theorem, we examine two scenarios: in the first, the monotonic sequence is bounded; in the second, it is unbounded.

Case 1 (Bounded and Increasing Sequence)

Consider a monotonic, increasing, and bounded sequence.

Given any ε > 0, there exists an index v such that for all n > v:

$$ l - \epsilon < a_v \le a_n \le l < l + \epsilon $$

This inequality becomes clearer when visualized on a Cartesian plane:

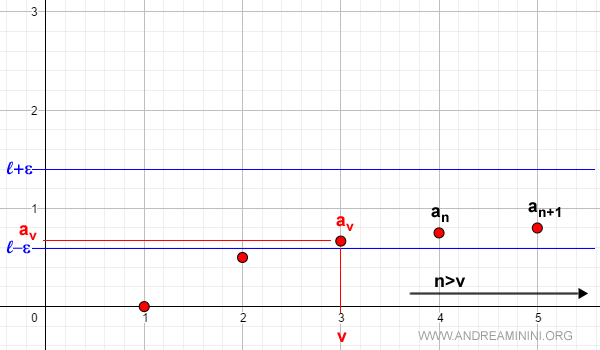
Hence, as n approaches infinity, the sequence converges to l = 1:

$$ \lim_{n \rightarrow \infty} a_n = 1 $$

Case 2 (Unbounded and Increasing Sequence)

Now consider a monotonic, increasing, and unbounded sequence.

Since it lacks an upper bound, for any chosen M > 0, there exists an index v > 0 such that for all n > v:

$$ a_n \ge a_v > M $$

This inequality becomes much clearer when visualized on a Cartesian plane:

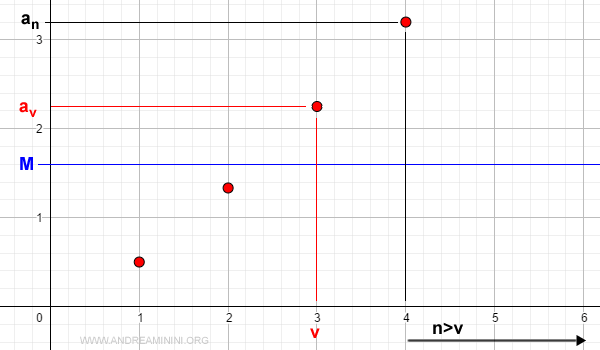
Therefore, as n approaches infinity, the sequence diverges to infinity:

$$ \lim_{n \rightarrow \infty} a_n = +\infty $$

Note. The proof for monotonic decreasing sequences, whether bounded or unbounded, follows the same reasoning as for increasing sequences.

And so on.