Monotonic Increasing and Decreasing Sequences

monotonic

strictly increasing
if each term is greater than the one preceding it: $$ a_{n+1} > a_n $$
non-decreasing
if each term is greater than or equal to the one before it: $$ a_{n+1} \ge a_n $$
strictly decreasing
if each term is less than the one preceding it: $$ a_{n+1} < a_n $$
non-increasing
if each term is less than or equal to the one before it: $$ a_{n+1} \le a_n $$

These definitions can vary slightly depending on the textbook.

For instance, some books refer to non-decreasing or non-increasing sequences as increasing or decreasing “in the broad sense.”

Note. A sequence is said to be constant if every term is equal to the previous one: $$ a_{n+1} = a_n $$

A Practical Example

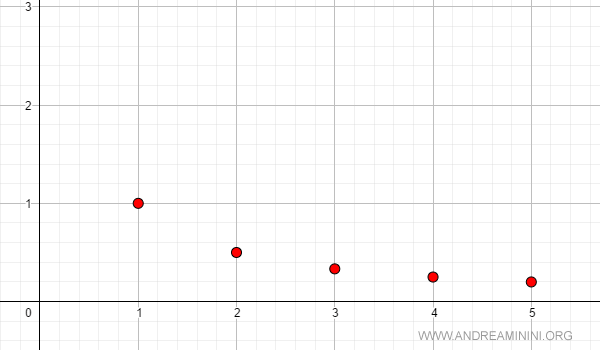
Example 1

The following sequence is strictly decreasing:

$$ a_n = \frac{1}{n} $$

because for every n ∈ N:

$$ a_{n+1} < a_n $$

$$ \frac{1}{n+1} < \frac{1}{n} $$

Here’s how the sequence appears in a Cartesian plot:

an example of a strictly decreasing monotonic sequence

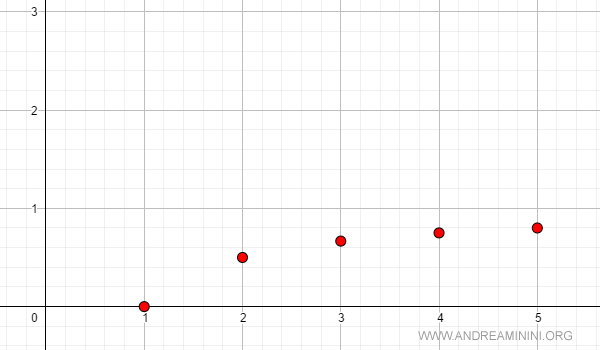
Example 2

The following sequence is strictly increasing:

$$ a_n = \frac{n-1}{n} $$

because for every n ∈ N:

$$ a_{n+1} > a_n $$

In particular:

$$ \frac{n-1+1}{n+1} > \frac{n-1}{n} $$

which simplifies to:

$$ \frac{n}{n+1} > \frac{n-1}{n} $$

and ultimately to:

$$ \frac{1}{n(n+1)} > 0 $$

Here’s the graph of this sequence:

an example of a strictly increasing sequence

A sequence is constant if, for every n in N: $$ a_{n+1} = a_n $$

Constant sequences are a special case of both increasing and decreasing sequences.

And so on.