Divergent Sequences

A sequence a_n is called divergent (or infinite) if its limit is equal to +∞. $$ \lim_{ n \rightarrow +\infty } a_n = +\infty $$ In other words, for every M > 0, there exists a natural number v such that a_n > M for all n > v. $$ \forall M > 0, \exists v : a_n > M \:\: \forall n > v $$

Similarly, a sequence is also considered divergent if its limit equals -∞.

A sequence a_n is said to be negatively divergent if its limit is -∞. $$ \lim_{ n \rightarrow +\infty } a_n = -\infty $$ This means that for every M > 0, there exists a natural number v such that a_n < -M for all n > v. $$ \forall M > 0, \exists v : a_n < -M \:\: \forall n > v $$

Some Practical Examples

Example 1

Consider the sequence x²:

$$ a_n = x^2 $$

This sequence diverges to positive infinity because its limit as n approaches infinity is +∞:

$$ \lim_{n \rightarrow +\infty} x^2 = +\infty $$

The first few terms of the sequence are: $$ a_n = \{ 1, 4, 9, 16, \dots , +\infty \} $$

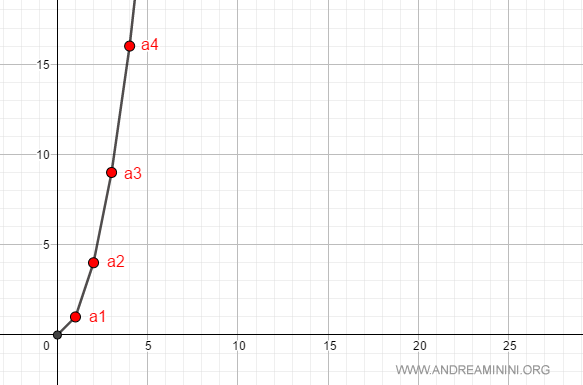
For instance, if we choose M = 10, there exists a natural number v = 3 (since a_v = a₃ = 9) such that for all n > 3, we have a_n > 10.

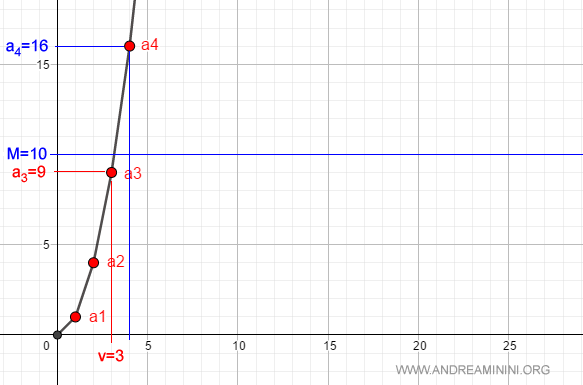
This holds true for any other value of M > 0.

Example 2

Consider the sequence 1 - x²:

$$ a_n = 1 - x^2 $$

This sequence diverges to negative infinity because its limit as n approaches infinity is -∞:

$$ \lim_{n \rightarrow +\infty} 1 - x^2 = -\infty $$

The first few terms of the sequence are: $$ a_n = \{ 0, -3, -8, -15, \dots , -\infty \} $$

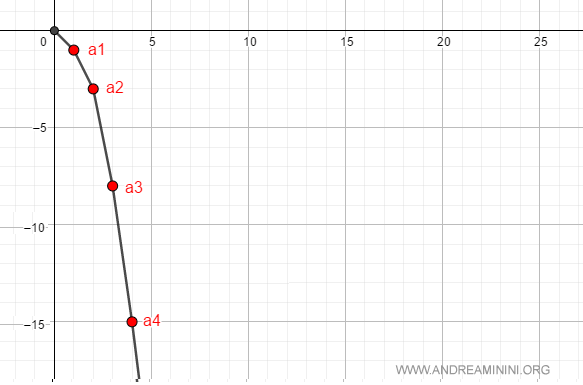
For example, if we pick M = 10, there exists a natural number v = 3 (where a_v = a₃ = -9) such that for all n > 3, we have a_n < -M; in other words, a_n < -10.

For instance, a₄ = -15 < -10.

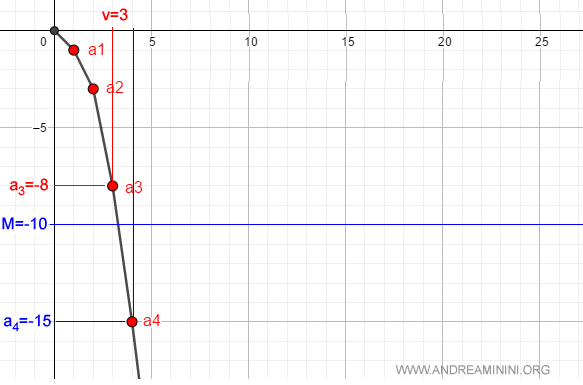
And so on.