Infinitesimal Sequences

A bounded sequence a_n is called infinitesimal if it converges to zero: $$ \lim_{n \rightarrow \infty} a_n = 0 $$

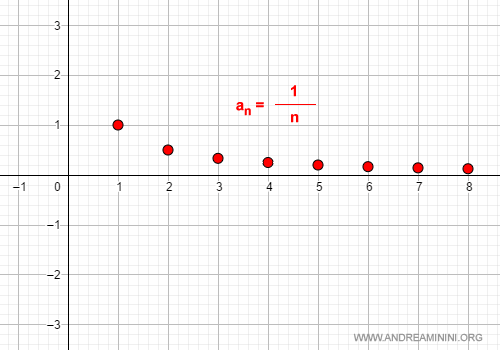
A Practical Example

Consider the sequence:

$$ a_n = \frac{1}{n} $$

This sequence approaches zero as n tends to infinity:

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

Therefore, it qualifies as an infinitesimal sequence.

Properties of Infinitesimal Sequences

A sequence a_n converges to zero if and only if its absolute value |a_n| also converges to zero: $$ \lim_{n \rightarrow \infty} a_n = 0 \Rightarrow \lim_{n \rightarrow \infty} |a_n| = 0 $$

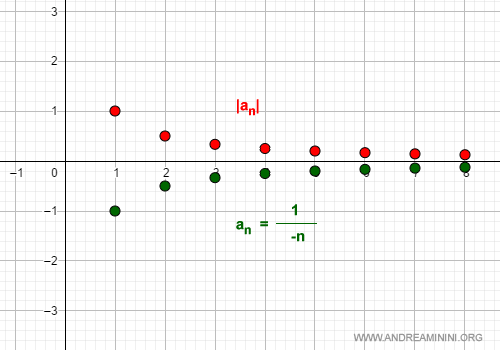
Example

The following sequence a_n is infinitesimal:

$$ a_n = \frac{1}{-n} $$

because it converges to zero as n approaches infinity:

$$ \lim_{n \rightarrow \infty} \frac{1}{-n} = 0 $$

Its absolute value |a_n| likewise converges to zero:

$$ \lim_{n \rightarrow \infty} \left| \frac{1}{-n} \right| = 0 $$

Proof

Let’s define the absolute value of the sequence a_n as a separate sequence b_n:

$$ b_n = |a_n| $$

According to the definition of a limit, a sequence converges if:

$$ \forall \epsilon > 0, \exists v : |b_n - l| < \epsilon \quad \forall n > v $$

In the case of an infinitesimal sequence, l = 0, so this condition becomes:

$$ \forall \epsilon > 0, \exists v : |b_n| < \epsilon \quad \forall n > v $$

Since |b_n| = ||a_n|| = |a_n|,

it follows that the convergence of the absolute value of a_n to zero is equivalent to the sequence itself being infinitesimal.

And so on.