Neighborhood in Mathematics

A neighborhood is an open interval that contains a point x₀.
$$ (x_0-\delta, \, x_0+\delta) $$

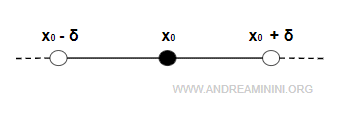
Typically, a neighborhood is an open interval that does not include its endpoints.

A Practical Example

Suppose the point x₀ equals ten:

$$ x_0 = 10 $$

and we choose delta equal to two:

$$ \delta = 2 $$

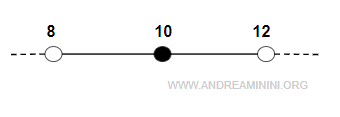
Then the neighborhood is the interval extending from eight to twelve:

$$ (x_0-\delta, \, x_0+\delta) $$

$$ (10-2, \, 10+2) $$

$$ (8, 12) $$

This interval includes all numbers strictly between eight and twelve, excluding the endpoints.

Note. Unless otherwise specified, the point x₀ is considered part of the neighborhood. It may be located at the center of the interval, but this isn’t always the case. In some contexts, x₀ can even coincide with one of the interval’s endpoints.