Operations with Limits

Limits can be added, subtracted, multiplied, or divided. The following rules apply equally to limits of sequences and limits of functions.

Adding and Subtracting Limits

Given two limits as n → ∞: $$ \lim_{n \rightarrow +\infty } a_n = l_1 \\ \lim_{n \rightarrow +\infty } b_n = l_2 $$ where l₁ and l₂ are real numbers, then: $$ \lim_{n \rightarrow +\infty } \bigl( a_n + b_n \bigr) = l_1 + l_2 $$ and similarly: $$ \lim_{n \rightarrow +\infty } \bigl( a_n - b_n \bigr) = l_1 - l_2 $$

Example

Consider two sequences whose limits converge to +1 and +2, respectively:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 2 $$

Here’s how this looks graphically:

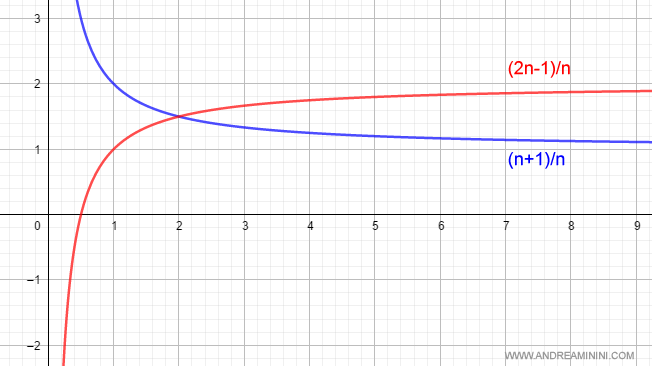
The sum of these two limits is 3:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} + \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 1 + 2 = 3 $$

Let’s quickly check this result directly:

$$ \lim_{n \rightarrow +\infty } \left( \frac{n+1}{n} + \frac{2n-1}{n} \right) $$

$$ \lim_{n \rightarrow +\infty } \frac{n+1+2n-1}{n} $$

$$ \lim_{n \rightarrow +\infty } \frac{3n}{n} = 3 $$

And indeed, that’s correct.

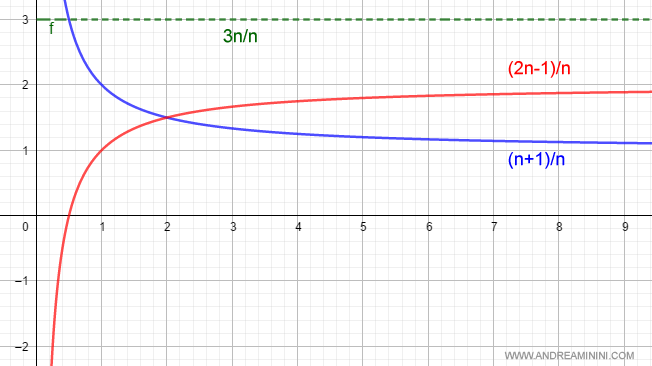
Therefore, the limit of a sum equals the sum of the individual limits of the sequences or functions involved.

Proof

For any ε > 0, there exists a value v₁ such that:

$$ \forall \epsilon > 0 \; \exists \; v_1 : |a_n - l_1| < \epsilon, \; \forall n > v_1 $$

The same statement holds for the second sequence:

$$ \forall \epsilon > 0 \; \exists \; v_2 : |b_n - l_2| < \epsilon, \; \forall n > v_2 $$

Example

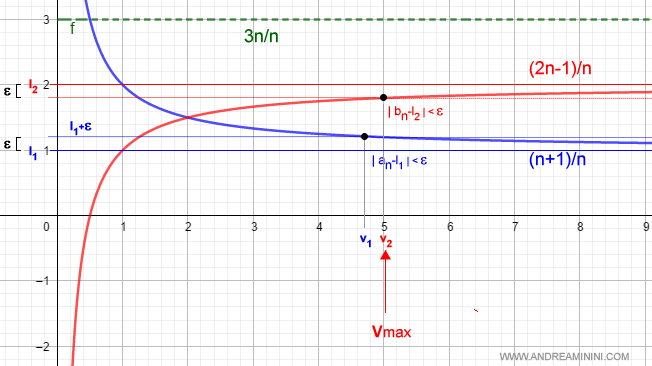
We take the maximum of v₁ and v₂:

Choosing this maximum ensures that both conditions are simultaneously satisfied for all n > v:

$$ v = \max(v_1, v_2) $$

Example. In the earlier example, the condition for the first sequence (blue) was n > 4.7, while for the second sequence (red) it was n > 5. So for n > 5, both conditions are satisfied.

Therefore, for every n > v, the sum of the two sequences satisfies:

$$ |(a_n + b_n) - (l_1 + l_2)| < 2\epsilon $$

We can rewrite the absolute value as follows:

$$ |(a_n - l_1) + (b_n - l_2)| < 2\epsilon $$

Applying the triangle inequality yields:

$$ |(a_n - l_1) + (b_n - l_2)| \le |a_n - l_1| + |b_n - l_2| $$

So the right-hand side becomes the sum of the individual differences.

Since:

$$ |a_n - l_1| < \epsilon \\ |b_n - l_2| < \epsilon $$

we conclude:

$$ |(a_n - l_1) + (b_n - l_2)| \le |a_n - l_1| + |b_n - l_2| < \epsilon + \epsilon $$

$$ |(a_n - l_1) + (b_n - l_2)| < 2\epsilon $$

This completes the proof that the sum of two limits equals the limit of the sum of the corresponding sequences or functions - and the same holds in reverse.

Multiplying Two Limits

Given two limits as n → ∞: $$ \lim_{n \rightarrow +\infty } a_n = l_1 \\ \lim_{n \rightarrow +\infty } b_n = l_2 $$ where l₁ and l₂ are real numbers, then: $$ \lim_{n \rightarrow +\infty } \bigl( a_n \cdot b_n \bigr) = \lim_{n \rightarrow +\infty } a_n \cdot \lim_{n \rightarrow +\infty } b_n = l_1 \cdot l_2 $$

Example

Consider two sequences converging respectively to +1 and +2:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 2 $$

Here’s the graphical representation:

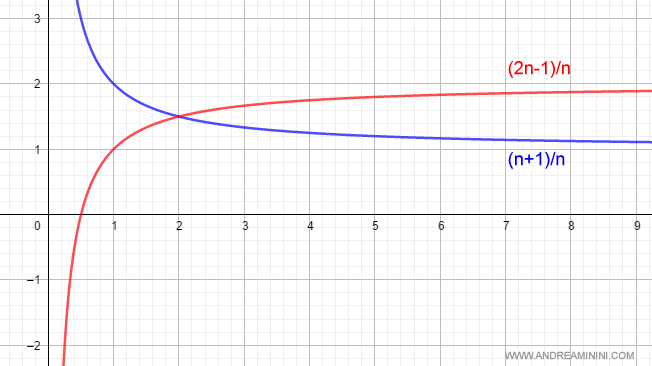
According to the rule, the product of these limits equals 2:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} \cdot \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 1 \cdot 2 = 2 $$

Let’s verify this directly:

$$ \lim_{n \rightarrow +\infty } \left( \frac{n+1}{n} \cdot \frac{2n-1}{n} \right) $$

$$ \lim_{n \rightarrow +\infty } \frac{(n+1)\cdot(2n-1)}{n^2} $$

$$ \lim_{n \rightarrow +\infty } \frac{2n^2 + n - 1}{n^2} = \frac{\infty}{\infty} $$

Since this is an indeterminate form ∞/∞, we apply L’Hôpital’s Rule:

$$ \lim_{n \rightarrow +\infty } \frac{2n^2 + n - 1}{n^2} = \lim_{n \rightarrow +\infty } \frac{4n + 1}{2n} = \lim_{n \rightarrow +\infty } \frac{4}{2} = 2 $$

And our result checks out perfectly.

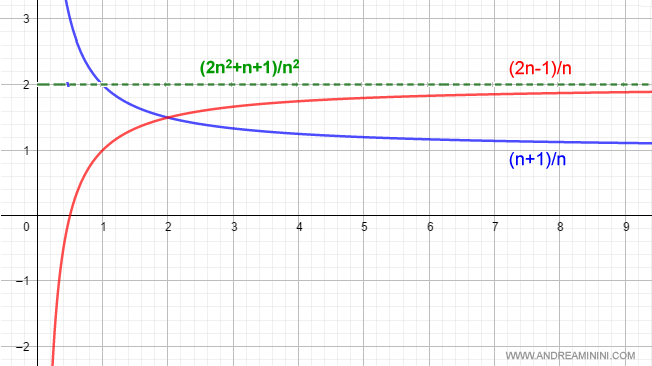
So the limit of the product equals the product of the limits of the sequences or functions involved.

Proof

By the definition of the limit of a sequence, a sequence is bounded if there exists a real number M such that:

$$ |a_n| \le M \quad \forall \, n \in \mathbb{N} $$

For any ε > 0, there exists a value v₁ such that:

$$ \forall \epsilon > 0 \; \exists \; v_1 : |a_n - l_1| < \epsilon, \quad \forall n > v_1 $$

The same statement holds for the second sequence:

$$ \forall \epsilon > 0 \; \exists \; v_2 : |b_n - l_2| < \epsilon, \quad \forall n > v_2 $$

We then select the greater of the two indices:

$$ v = \max(v_1, v_2) $$

For all n > v, the product of the two sequences must satisfy:

$$ |(a_n \cdot b_n) - (l_1 \cdot l_2)| < \epsilon \cdot \epsilon $$

To proceed, we add and subtract \( a_n \cdot l_2 \) inside the absolute value:

$$ |(a_n \cdot b_n) - (l_1 \cdot l_2) + (a_n \cdot l_2) - (a_n \cdot l_2)| < \epsilon \cdot \epsilon $$

Rewriting and grouping terms, we obtain:

$$ |a_n \cdot (b_n - l_2) + l_2 \cdot (a_n - l_1)| < \epsilon \cdot \epsilon $$

Applying the triangle inequality gives:

$$ |a_n \cdot (b_n - l_2) + l_2 \cdot (a_n - l_1)| \le |a_n| \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| $$

Since \( |a_n| \le M \), this simplifies to:

$$ |a_n \cdot (b_n - l_2) + l_2 \cdot (a_n - l_1)| \le M \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| $$

Thus, the deviation of the product from its limit is bounded by the sum on the right.

Given that \( |a_n - l_1| < \epsilon \) and \( |b_n - l_2| < \epsilon \), we can write:

$$ |a_n \cdot (b_n - l_2) + l_2 \cdot (a_n - l_1)| \le M \cdot \epsilon + |l_2| \cdot \epsilon $$

Since ε > 0, the absolute value around ε can be dropped, yielding:

$$ |a_n \cdot (b_n - l_2) + l_2 \cdot (a_n - l_1)| < \epsilon \cdot (M + |l_2|) $$

By choosing ε small enough, we ensure that the product converges. For instance, if we set:

$$ \epsilon = \frac{\delta}{M + |l_2|} $$

we can make the left-hand side as small as desired, completing the proof that:

$$ \forall \delta > 0 \; \exists \; v : |a_n \cdot b_n - l_1 \cdot l_2| < \delta, \quad \forall n > v $$

Dividing Two Limits

Given two limits as n → ∞: $$ \lim_{n \rightarrow +\infty } a_n = l_1 \\ \lim_{n \rightarrow +\infty } b_n = l_2 $$ where l₁ and l₂ are real numbers, the limit of their quotient is: $$ \lim_{n \rightarrow +\infty } \frac{a_n}{b_n} = \frac{\lim_{n \rightarrow +\infty } a_n}{\lim_{n \rightarrow +\infty } b_n} = \frac{l_1}{l_2} $$ provided that \( l_2 \neq 0 \).

Example

Consider two sequences converging respectively to +1 and +2:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 2 $$

Here’s how this looks graphically:

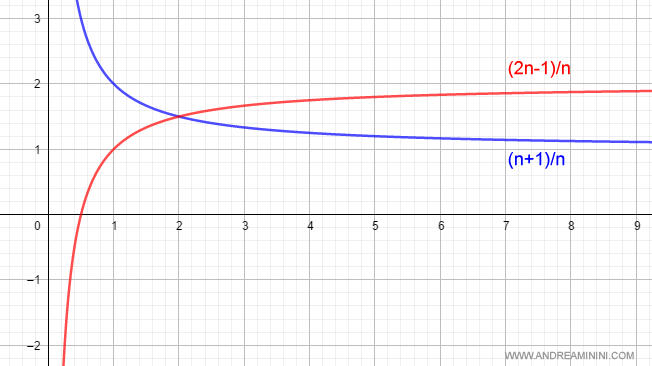
According to the rule above, the quotient of these two limits is:

$$ \frac{\lim_{n \rightarrow +\infty } \frac{n+1}{n}}{\lim_{n \rightarrow +\infty } \frac{2n-1}{n}} = \frac{1}{2} $$

Let’s verify this directly:

$$ \lim_{n \rightarrow +\infty } \frac{\frac{n+1}{n}}{\frac{2n-1}{n}} $$

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} \cdot \frac{n}{2n-1} $$

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{2n-1} = \frac{\infty}{\infty} $$

Since this is an indeterminate form ∞/∞, we apply L’Hôpital’s Rule:

$$ \lim_{n \rightarrow +\infty } \frac{1}{2} = \frac{1}{2} $$

And indeed, the result is correct.

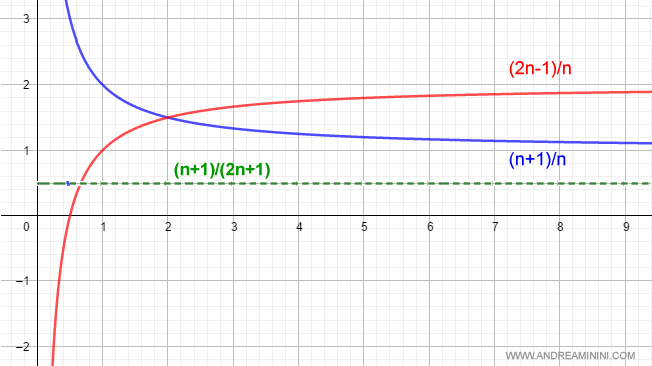
Therefore, the limit of a quotient equals the quotient of the limits of the functions or sequences, provided the denominator’s limit is not zero.

And so on.