Criterion for the Invertibility of Functions

A function that is continuous and strictly monotonic over an interval [a,b] is an invertible function on that same interval. $$ y = f(x) \: \forall x \in [a,b] $$ $$ x = f^{-1}(y) \: \forall y \in [f(a),f(b)] $$

Therefore, on the interval [a,b], there exists an inverse function, commonly denoted as f^-1.

A Practical Example

Consider the following function, which is continuous and strictly monotonic on the interval [0,5]:

$$ f(x) = 2x $$

Here’s its graph:

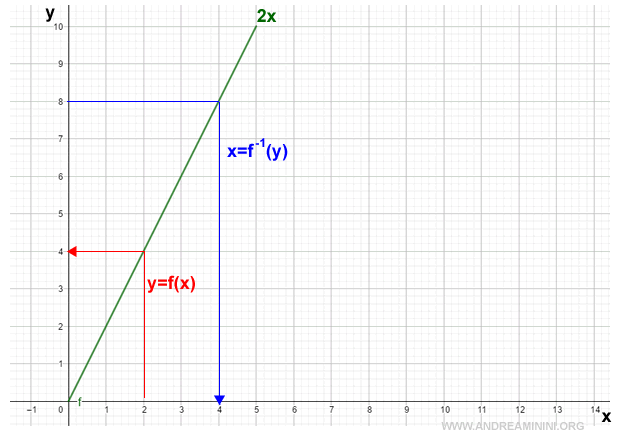
Hence, the function is invertible over the interval [0,5].

$$ y = 2x $$

$$ x = \frac{y}{2} $$

The inverse function is given by:

$$ f^{-1}(y) = \frac{y}{2} = x $$

For each value \( y_0 \) in the image Im(f), there exists one and only one value \( x_0 \) within the interval [0,5] such that \( f(x_0) = y_0 \).

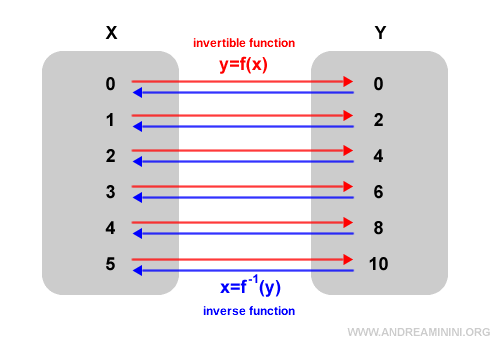
Proof Explained

Let’s examine a strictly increasing function defined on the interval [a,b]:

$$ f(a) < f(x) < f(b) \: \forall x \in (a,b) $$

Because the function is strictly increasing, it’s clear that f(a) represents its minimum value and f(b) its maximum.

According to the Intermediate Value Theorem, any function that’s continuous on a closed interval [a,b] takes on every value between its minimum f(a) and its maximum f(b).

$$ y \in [ f(a), f(b) ] $$

Therefore, for each value \( y \) in [f(a), f(b)], there exists a value \( x \) in [a,b] such that:

$$ \forall y \in [ f(a), f(b) ] \: \exists \: x \in [a,b] \: : \: f(x) = y $$

Now, we need to establish that this value of x is unique.

Why? An invertible function must associate exactly one value of x in its domain with each value of y in its codomain. Therefore, we need to show that for every y in [f(a), f(b)], there is one and only one x in [a,b] such that f(x)=y.

Let’s argue by contradiction. Suppose there exist two distinct values \( x_1 \) and \( x_2 \), with \( x_1 < x_2 \), such that:

$$ f(x_1) = f(x_2) = y $$

Since \( x_1 \) and \( x_2 \) are distinct, and because the function is strictly increasing, it would follow that:

$$ f(x_1) < f(x_2) $$

Why? According to the criterion for strict monotonicity, a function f(x) is strictly increasing if it rises continuously across every point x within the interval [a,b]. It cannot decrease or remain constant at any point.

But this contradicts our assumption that \( f(x_1) = f(x_2) = y \).

Thus, for a strictly increasing function, the equality \( f(x_1) = f(x_2) \) implies \( x_1 = x_2 \).

Consequently, there is exactly one x-value corresponding to each y-value, and vice versa.

$$ f:[a,b] \Leftrightarrow f:[f(a),f(b)] $$

The uniqueness of x is therefore proven.

This confirms the invertibility of any function that is continuous and strictly monotonic over the interval [a,b].

And so on.