Squeeze Theorem

Consider three sequences a_n, b_n, and c_n. If for every n > 0 we have $$ a_n \le b_n \le c_n $$ and if both sequences a_n and c_n converge to the same limit l, namely $$ \lim_{n \rightarrow \infty} a_n = \lim_{n \rightarrow \infty} c_n = l $$ then the sequence b_n also converges to l. $$ \lim_{n \rightarrow \infty} b_n = l $$

This result is a classic example of a comparison theorem used in the study of sequence limits.

The same principle extends naturally to limits of functions.

A Practical Example

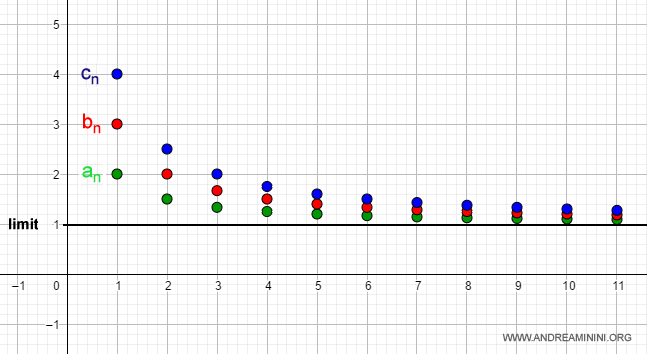
Let’s look at the following three sequences:

$$ a_n = \frac{n+1}{n} $$

$$ b_n = \frac{n+2}{n} $$

$$ c_n = \frac{n+3}{n} $$

which satisfy the order relation:

$$ a_n \le b_n \le c_n $$

The limits of both a_n and c_n are equal to 1:

$$ \lim_{n \rightarrow \infty} \frac{n+1}{n} = 1 $$

$$ \lim_{n \rightarrow \infty} \frac{n+3}{n} = 1 $$

Note. These two limits are examples of an indeterminate form of the type ∞/∞, which can be easily evaluated using L'Hôpital's Rule.

By the Squeeze Theorem, it follows that the intermediate sequence b_n must also converge to 1:

$$ \lim_{n \rightarrow \infty} \frac{n+2}{n} = 1 $$

And indeed, it does.

Why is it called the Squeeze Theorem? It’s called the Squeeze Theorem because it describes how a sequence (or a function) “gets squeezed” between two others. If the two outer sequences both approach the same limit, then the one trapped between them has no choice but to go to that same limit as well. The imagery is like having two barriers closing in on a value, forcing the middle sequence toward a single outcome. The name vividly conveys this idea of “pinning down” the behavior of the middle sequence by comparing it to its upper and lower bounds.

Proof

By hypothesis, for every ε > 0, there exist values v₁ and v₂ such that:

$$ \exists v_1 \;\; \text{such that} \;\; |a_n - l| < \epsilon \quad \forall n > v_1 $$

$$ \exists v_2 \;\; \text{such that} \;\; |c_n - l| < \epsilon \quad \forall n > v_2 $$

We can express these absolute value inequalities in terms of intervals as follows:

$$ l - \epsilon < a_n < l + \epsilon $$

$$ l - \epsilon < c_n < l + \epsilon $$

Now, let’s choose the maximum of v₁ and v₂:

$$ v = \max(v_1, v_2) $$

With this choice, both inequalities hold for all n > v.

Therefore, we have the combined inequality:

$$ l - \epsilon < a_n \le b_n \le c_n < l + \epsilon $$

By isolating b_n we obtain:

$$ l - \epsilon < b_n < l + \epsilon $$

And finally, this can be rewritten using absolute value:

$$ |b_n - l| < \epsilon \quad \forall n > v $$

This establishes that the sequence b_n also converges to l.

And so on.