Decreasing function

A function y=f(x) is said to be decreasing on an interval I=(a,b) if, for any two points x₁, x₂ in the interval with x₁<x₂, we have $$ f(x_1) \ge f(x_2) $$. It is called strictly decreasing if, instead, $$ f(x_1) > f(x_2) $$.

A strictly decreasing function is often described as “decreasing in the strict sense.”

Both decreasing and strictly decreasing functions belong to the wider class of monotone functions.

Note. A function is monotone on an interval of its domain if, throughout that interval, it is consistently either non-decreasing or non-increasing.

Example

Consider the function

$$ y=x^2 $$

This function is strictly decreasing on the interval (-4,0), because for any two points x₁<x₂ within that interval we have f(x₁)>f(x₂).

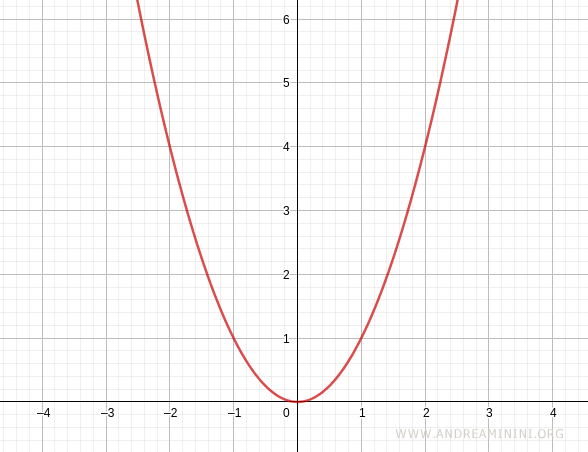
By contrast, the same function is not decreasing on the interval (0,4).

Note. The monotonic behavior of a continuous, differentiable function can also be determined by examining the sign of its first derivative, f'(x).

And so on.