Concave and Convex Functions
Convex Function
A function $f(x)$ is said to be convex on an interval $[a, b]$ if, for every point $x_0 \in [a, b]$, the graph of the function over $[a, b]$ lies above the tangent line at the point $(x_0, f(x_0))$.
Concave Function
A function $f(x)$ is said to be concave on an interval $[a, b]$ if, for every point $x_0 \in [a, b]$, the graph of the function over $[a, b]$ lies below the tangent line at the point $(x_0, f(x_0))$.
In the sections below, I’ll explain how to determine whether a function is concave or convex, either by examining its graph or by analyzing its derivative.
How to identify whether a function is concave or convex
Given a function defined on an interval $[a, b]$ and a point $x_0$ within that interval, we can classify the function as follows:
- Convex, if its graph over $[a, b]$ lies above the tangent line at $(x_0, f(x_0))$

- Concave, if its graph over $[a, b]$ lies below the tangent line at $(x_0, f(x_0))$

A function can be concave or convex throughout its entire domain, or only over certain portions of it.
In fact, it is quite common for a function to exhibit concavity in some intervals and convexity in others.

The transition between concavity and convexity (and vice versa) occurs at points known as inflection points.
What are inflection points?
An inflection point occurs at $x_0$ if the tangent line lies below the graph of the function to the left of $x_0$ and above it to the right of $x_0$, marking a transition from convexity to concavity, or the reverse.
For example, in the graph below, the point $f_A$ is an inflection point where the function transitions from concavity to convexity.
To the left of point $f_A$, the graph of the function (red curve) lies below the tangent line (blue line). To the right of $f_A$, it lies above.
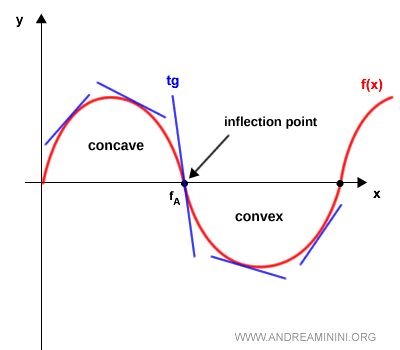
The opposite scenario can also occur.
If the tangent line lies below the graph of the function to the left of $x_0$ and above it to the right of $x_0$, then $x_0$ is again an inflection point, this time marking a transition from convexity to concavity.
For instance, at point $f_B$ in the graph below, the function transitions from convexity to concavity.
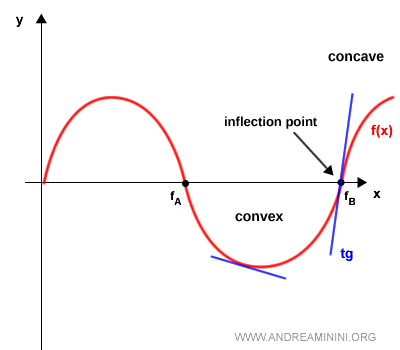
In this case, the graph of the function (red curve) lies below the tangent line (blue line) before point $f_B$, and above it afterward.
Criterion for Concavity and Convexity
You can determine whether a function is convex or concave without even looking at its graph - simply by analyzing its derivatives.
Convexity Criterion
If the first derivative $f'(x)$ is increasing on an interval $[a, b]$, then the function $f(x)$ is convex over that interval. Equivalently, the function is convex if its second derivative is non-negative: $$ f''(x) \ge 0 \quad \forall x \in (a, b) $$
In short, saying that $f'(x)$ is increasing is equivalent to saying that $f''(x) \ge 0$.
$$ f''(x) \ge 0 $$
By applying the monotonicity criterion to the first derivative, we see that $f''(x)$ is non-negative whenever $f'(x)$ is increasing:
$$ f''(x) \ge 0 \quad \Leftrightarrow \quad f'(x)\ \text{is increasing} $$
Example
The function $f(x) = x^2$ is convex at $x = 0$, since its first derivative $f'(x) = 2x$ is increasing in the neighborhood of $x = 0$.
Since $f'(x)$ is increasing, it follows that $f''(x) \ge 0$ near $x = 0$.

This confirms that the function is convex at $x = 0$, as any tangent line at that point lies below the curve.
Concavity Criterion
If the first derivative $f'(x)$ is decreasing on an interval $[a, b]$, then the function $f(x)$ is concave on that interval. In other words, $f(x)$ is concave if its second derivative is non-positive: $$ f''(x) \le 0 \quad \forall x \in (a, b) $$
Again, saying that $f'(x)$ is decreasing is equivalent to stating that $f''(x) \le 0$:
$$ f''(x) \le 0 $$
Thus, applying the monotonicity criterion to $f'(x)$ yields:
$$ f''(x) \le 0 \quad \Leftrightarrow \quad f'(x)\ \text{is decreasing} $$
Example
The function $f(x) = \log x$ is concave at $x = 3$, since its first derivative $f'(x) = 1/x$ is decreasing in a neighborhood of $x = 3$.
Since $f'(x)$ is decreasing, $f''(x) \le 0$ near $x = 3$.

This confirms that the function is concave at $x = 3$, as the tangent line lies above the curve at that point.
Proof of the Convexity and Concavity Criteria
The proof proceeds in two parts:
- If $f(x)$ is convex, then $f'(x)$ is increasing.
- If $f'(x)$ is increasing, then $f(x)$ is convex.
Note: The concavity criterion can be demonstrated in exactly the same way.
Proof - Part 1
Assume that $f(x)$ is convex. We will show that $f'(x)$ is increasing.
Let $f(x)$ be defined on $[a, b]$, and select two points $x_1 < x_2$ within this interval.
Since the function is convex, the graph of $f(x)$ lies above the tangent line at both $x_1$ and $x_2$:
$$ f(x) \ge f(x_1) + f'(x_1)(x - x_1) $$
$$ f(x) \ge f(x_2) + f'(x_2)(x - x_2) $$
for any $x \in [a, b]$.
Note: The right-hand side represents the tangent line at $x_1$ or $x_2$.

Now, evaluate the first inequality at $x = x_2$, and the second at $x = x_1$:
$$ f(x_2) \ge f(x_1) + f'(x_1)(x_2 - x_1) $$
$$ f(x_1) \ge f(x_2) + f'(x_2)(x_1 - x_2) $$
Graphically:

Adding the two inequalities:
$$ 0 \ge f'(x_1)(x_2 - x_1) + f'(x_2)(x_1 - x_2) $$
Rewriting:
$$ [f'(x_2) - f'(x_1)](x_2 - x_1) \ge 0 $$
Since $x_2 - x_1 > 0$, it follows that:
$$ f'(x_2) - f'(x_1) \ge 0 \quad \forall x \in (x_1, x_2) $$
In other words, $f'(x)$ is increasing on $[x_1, x_2]$. By the monotonicity criterion, if $f'(x)$ is increasing, then $f''(x) \ge 0$ on $[x_1, x_2]$:
$$ f''(x) \ge 0 \quad \forall x \in (x_1, x_2) $$
This proves that if $f(x)$ is convex, then $f'(x)$ is increasing and $f''(x) \ge 0$.
Proof - Part 2
Now, let us prove the converse: if $f'(x)$ is increasing, then $f(x)$ is convex.
Take any two distinct points $x$ and $x_0$ in $[a, b]$:
$$ x \ne x_0 $$
By the Mean Value Theorem, there exists a point $x_1$ between $x$ and $x_0$ such that:
$$ f'(x_1) = \frac{f(x) - f(x_0)}{x - x_0} $$
or equivalently:
$$ f(x) - f(x_0) = f'(x_1)(x - x_0) $$
Since $f'(x)$ is increasing on $[a, b]$, we analyze two cases:
- Case 1: $x < x_0$ Then $(x - x_0) < 0$ and $x_1 \in (x, x_0)$, so $x_1 < x_0$. Since $f'(x)$ is increasing: $$ f'(x_1) \le f'(x_0) $$ Multiplying by $(x - x_0)$ (which is negative) reverses the inequality: $$ f'(x_1)(x - x_0) \ge f'(x_0)(x - x_0) $$ Substituting: $$ f(x) - f(x_0) \ge f'(x_0)(x - x_0) $$
- Case 2: $x > x_0$ Then $(x - x_0) > 0$ and $x_1 \in (x_0, x)$, so $x_1 > x_0$. Since $f'(x)$ is increasing: $$ f'(x_1) \ge f'(x_0) $$ Multiplying by $(x - x_0) > 0$ does not change the inequality: $$ f'(x_1)(x - x_0) \ge f'(x_0)(x - x_0) $$ Substituting: $$ f(x) - f(x_0) \ge f'(x_0)(x - x_0) $$
In both cases we obtain:
$$ f(x) \ge f(x_0) + f'(x_0)(x - x_0) $$
The right-hand side is the equation of the tangent line at $x_0$.
Since the function lies above its tangent line, it is convex.
And so on.
