Lagrange’s Theorem

Statement of Lagrange’s Theorem

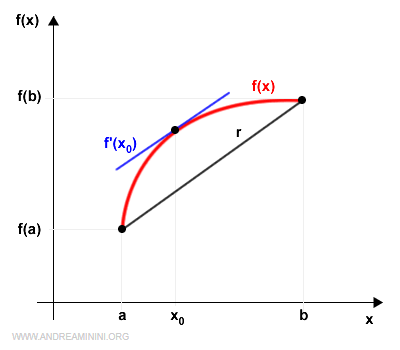
Let f(x) be a function that is continuous on the interval [a,b] and differentiable on (a,b). Then there exists at least one point x in (a,b) such that the derivative f'(x₀) equals the slope of the straight line connecting the endpoints a and b. $$ f'(x_0)=\frac{f(b)-f(a)}{b-a} $$

Lagrange’s Theorem is also known as the Mean Value Theorem of Differential Calculus.

A Practical Example

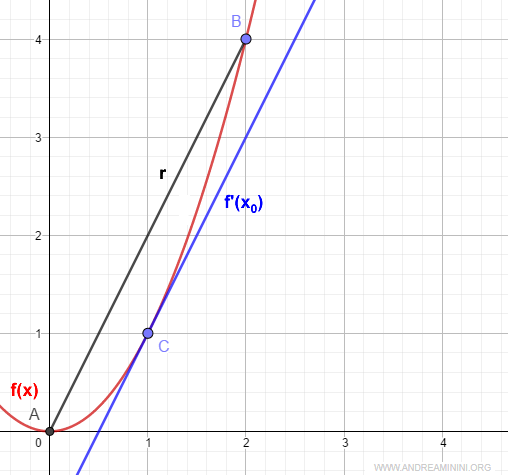
Consider the function f(x) = x², which is continuous on the interval [0,2] and differentiable on (0,2).

$$ f(x)=x^2 $$

The point where Lagrange’s Theorem applies satisfies:

$$ f'(x_0) = \frac{f(b)-f(a)}{b-a} $$

Since the derivative of f(x)=x² is f'(x)=2x, we have:

$$ 2x_0 = \frac{f(b)-f(a)}{b-a} $$

Given the endpoints a=0 and b=2, it follows that:

$$ 2x_0 = \frac{f(2)-f(0)}{2-0} $$

$$ 2x_0 = \frac{4-0}{2-0} $$

$$ 2x_0 = 2 $$

Therefore, the point x₀ equals 1:

$$ x_0 = \frac{2}{2} = 1 $$

At x₀ = 1, the derivative f'(x₀) matches the slope of the line connecting the endpoints [a,b].

Proof and Explanation

Let’s take a function f(x) that’s continuous on [a,b] and differentiable on (a,b).

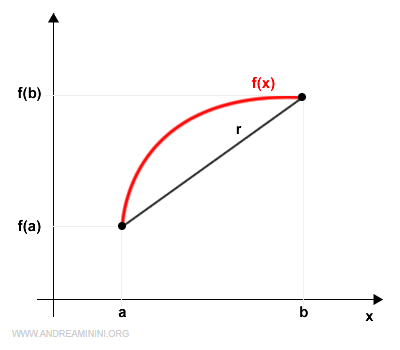
The equation of the line connecting the endpoints a and b is:

$$ r: f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) $$

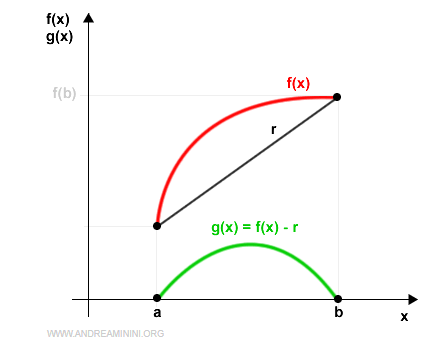
Here’s how it appears on a Cartesian plane:

Now, define a new function g(x) to represent the difference between f(x) and the line r:

$$ g(x) = f(x) - r $$

$$ g(x) = f(x) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$

This difference, f(x) - r, is zero at both endpoints a and b.

So, g(x) is also zero at those points.

Verification. At x = a, the function g(x) equals zero: $$ g(x) = f(x) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$ $$ g(a) = f(a) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (a - a) \right] $$ $$ g(a) = f(a) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot 0 \right] $$ $$ g(a) = f(a) - f(a) $$ $$ g(a) = 0 $$
At x = b, the function g(x) is also zero: $$ g(x) = f(x) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$ $$ g(b) = f(b) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (b - a) \right] $$ $$ g(b) = f(b) - \left[ f(a) + f(b) - f(a) \right] $$ $$ g(b) = f(b) - f(b) $$ $$ g(b) = 0 $$

Since g(x) is zero at both endpoints,

$$ g(a) = g(b) = 0 $$

by the Rolle’s Theorem, there must be at least one point x ∈ (a,b) where the derivative is zero:

$$ g'(x_0)=0 $$

Let’s differentiate g(x) on the interval (a,b):

$$ D[g(x)] = D\left[ f(x) - \left( f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right) \right] $$

$$ g'(x) = D[f(x)] - D\left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$

$$ g'(x) = f'(x) - \frac{f(b)-f(a)}{b-a} $$

Since g'(x) = 0 at x₀, we have:

$$ 0 = f'(x) - \frac{f(b)-f(a)}{b-a} $$

From this, it follows that the first derivative equals the slope of the line connecting a and b:

$$ f'(x) = \frac{f(b)-f(a)}{b-a} $$

Geometrically, the tangent line at x₀ - that is, the derivative f'(x₀) - shares the same slope as the secant line r.

We have thus proven Lagrange’s Theorem.

And so on.