Differentiability of a Function at a Point

A function is differentiable at a point c if the left-hand and right-hand limits of the difference quotient both exist and are equal. $$ f'(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x + Δx) - f(x)}{Δx} \\ \\ f'(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x + Δx) - f(x)}{Δx} $$

The left-hand limit of the difference quotient is called the left-hand derivative.

$$ f'(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x + Δx) - f(x)}{Δx} $$

Similarly, the right-hand limit is called the right-hand derivative.

$$ f'(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x + Δx) - f(x)}{Δx} $$

Two scenarios are possible:

If both limits exist and are equal, the function is differentiable at the point c.
If the two limits are not equal, the function is not differentiable at c.

Points where f(x) fails to be differentiable are known as singular points.

A Practical Example

Consider the absolute value function:

$$ f(x) = |x| $$

To determine whether it’s differentiable at x = 0, let’s first examine the right-hand limit.

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{f(x + Δx) - f(x)}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|x + Δx| - |x|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|0 + Δx - 0|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|Δx|}{Δx} = +1 $$

Since Δx approaches zero from the right, it remains positive, so the limit evaluates to +1.

Now, let’s compute the left-hand limit at x = 0:

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{f(x + Δx) - f(x)}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|x + Δx| - |x|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|0 + Δx - 0|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|Δx|}{Δx} = -1 $$

Here, Δx approaches zero from the left, so it’s negative, resulting in a limit of -1.

Conclusion

The left-hand and right-hand limits of the difference quotient at x = 0 are not equal:

$$ f'(0^+) = \lim_{Δx \rightarrow 0^+} \frac{|Δx|}{Δx} = +1 $$

$$ f'(0^-) = \lim_{Δx \rightarrow 0^-} \frac{|Δx|}{Δx} = -1 $$

Therefore, although the graph of the function meets at a single point, at x = 0, the function f(x) = |x| is not differentiable because the left-hand and right-hand limits differ (+1 ≠ -1).

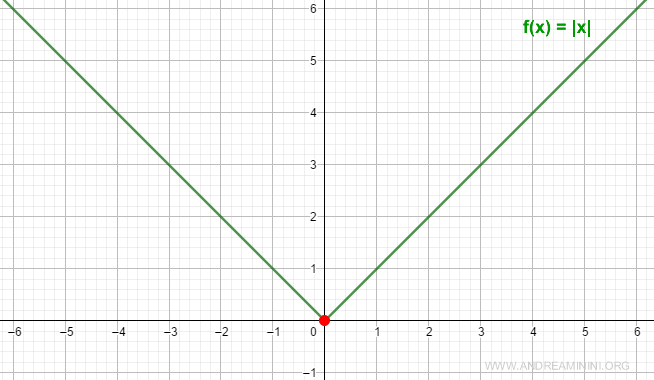
the function is not differentiable at x = 0

Note. This example also illustrates that continuity of a function at a point is a necessary condition for differentiability, but not sufficient. The function |x| is continuous at x = 0 but not differentiable there.

And so on.