Absolute Value Function

The absolute value function (also called the modulus function) is a function where the variable is placed inside absolute value bars. $$ f(x) = |x| $$

The absolute value function always returns the input as a non-negative number, that is, positive or zero.

For example, the absolute value of -3 is 3:

$$ | - 3 | = 3 $$

In other words, the function removes any negative sign from the input and returns its positive counterpart.

Absolute value is denoted by two vertical bars around the variable x:

$$ f(x) = |x| $$

Equivalently, it can be defined piecewise as:

$$ y=|x| = \begin{cases} x & \text{if } x \ge 0 \\ \\ -x & \text{if } x < 0 \end{cases} $$

This means the function equals:

• y = x when x is greater than or equal to zero,
• y = -x when x is less than zero.

In programming, it is often written as abs(), short for absolute value:

$$ y = abs(x) $$

You can also express absolute value as the square root of the square of the input: $$ y = |x| = \sqrt{x^2} $$

Why is it useful? Absolute value has many applications. A common one is calculating the distance between two points.

A Practical Example

Here are a few simple cases:

The absolute value of -3 is 3:

$$ | - 3 | = 3 $$

The absolute value of -4.2 is 4.2:

$$ | -4.2 | = 4.2 $$

The absolute value of 4 is 4:

$$\ |4| = 4 \ $$

The absolute value of -121 is 121:

$$\ |-121| = 121 \ $$

Note. The only special case is zero: since it has no sign, the absolute value of zero is simply zero. $$ |0| = 0 $$

The Graph of the Absolute Value Function

The graph of the absolute value function is always non-negative, so it lies entirely above (or on) the x-axis.

The classic example is f(x)=|x|, which looks like this on the Cartesian plane:

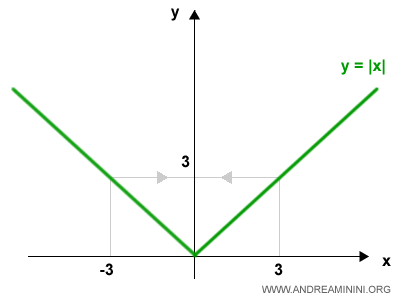
The function f(x)=|x| consists of two rays: y = x for x > 0 and y = -x for x < 0, which meet at the origin.

At the origin (0,0) the graph has a sharp corner. This means the function is continuous there but not differentiable.

Note. The argument inside the absolute value can be any expression. For instance, f(x)=|2x| or f(x)=|x²+1|. In such cases the graph may take different shapes, such as a parabola, depending on the input expression. For example, the graph of f(x)=|x³| resembles a parabola.

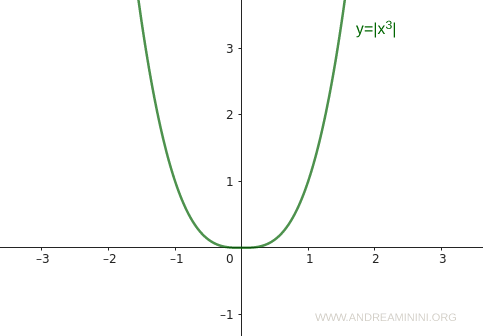
In every case, however, the graph remains entirely on or above the x-axis.

And so on.