Surjective Functions

What Is a Surjective Function?

A function is called surjective (or "onto") if every element of the codomain is the image of at least one element from the domain: $$ \forall \: y, \: \exists \: x \text{ such that } f(x) = y $$

Venn diagrams offer a helpful visual representation of surjectivity.

In a surjective function, each element of the codomain (B) is "covered" - that is, it corresponds to at least one input value from the domain (A).

Formally, a function $f$ is surjective if:

$$ \forall \ y \in B, \ \exists \ x \in A \text{ such that } f(x) = y $$

Note. It is not required that each $y \in B$ corresponds to exactly one $x \in A$; multiple inputs may map to the same output. What matters is that every element of the codomain is the image of some element in the domain.

In other words, every element in $B$ (the codomain) has at least one preimage in $A$ (the domain).

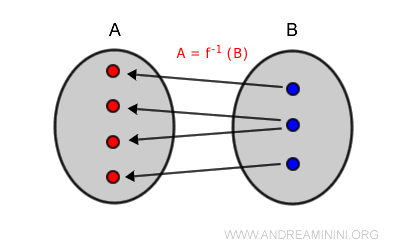
If a function is surjective, then the target set $B$ coincides exactly with its codomain.

This means that whether a function is surjective depends on how the codomain is defined.

Note. Any function can be made surjective by restricting its codomain to its image - the set of all actual output values of the function. For example, the function $f(x) = 2x$ is not surjective if the codomain is a set that includes 10, because 10 is not the double of any element in $A$.

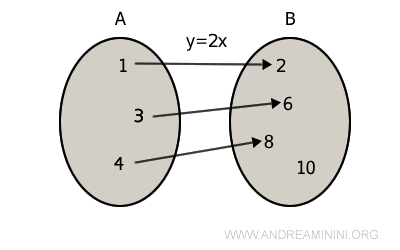
However, if we redefine the codomain to be the image $C = \{2, 6, 8\}$, then $f(x) = 2x$ becomes surjective.

Example

Consider a function that is surjective over the interval $y \in [a, b]$, because every $y$ value in that interval has at least one preimage $x$.

However, the same function is not surjective over $y \in [0, b]$, since the values in $[0, a]$ are not reached by any input $x$.

To make the function surjective, it suffices to restrict the codomain to the image of the function - i.e., $[a, b]$ instead of $[0, b]$.

Once the codomain is adjusted to match the actual range, the function becomes surjective.

A Practical Example

Example 1

Let the domain and codomain both be the set of real numbers $\mathbb{R}$:

$$ f: \mathbb{R} \rightarrow \mathbb{R} $$

The function

$$ f(x) = x + 1 $$

is surjective, because every real number $y$ can be expressed as $f(x)$ for some $x \in \mathbb{R}$.

x	y = f(x)
-3	-2
-2	-1
-1	0
0	1
1	2
2	3
3	4

Each output $y$ is associated with at least one input $x$.

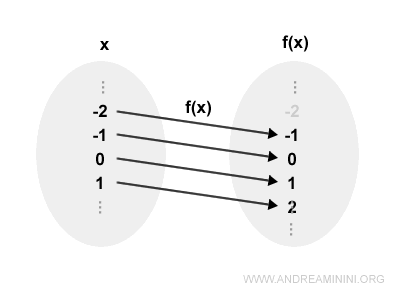
Therefore, $f(x) = x + 1$ is surjective over the set of real numbers.

Example 2

Again, define the domain and codomain as $\mathbb{R}$:

$$ f: \mathbb{R} \rightarrow \mathbb{R} $$

The function

$$ f(x) = x^2 $$

is not surjective, because certain values in the codomain $\mathbb{R}$ - such as negative numbers - cannot be obtained from any real input.

x	y = f(x)
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

For example, there is no $x$ such that $x^2 = -2$ or $x^2 = -3$.

Thus, $f(x) = x^2$ is not surjective if the codomain is $\mathbb{R}$.

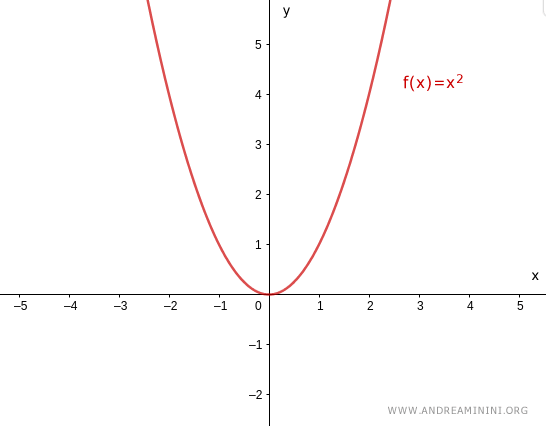
Note. To make $f(x) = x^2$ surjective, redefine the codomain as the set of non-negative real numbers: $$ f: \mathbb{R} \rightarrow \mathbb{R}^+ \cup \{0\} $$ With this choice, every $y \ge 0$ in the codomain has at least one corresponding $x$ in the domain.

And so on.