Differential Equations

What exactly is a differential equation?

A differential equation is an equation in which the unknown is a function, typically written as y = f(x), and the equation includes one or more derivatives of that function. $$ F(x, y, y', ..., y^{(k-1)}, y^{(n)}) = 0 $$ In essence, it's a relationship between a function y = f(x) and its derivatives. Here, y is the unknown function, \( y^{(n)} \) represents its derivatives, and x is the independent variable.

To be part of a differential equation, the functions involved must be continuous and differentiable up to order n - meaning they must admit n derivatives. This number n is called the order (or degree) of the differential equation.

Note. When a function is continuous and differentiable n times, we say it belongs to class Cⁿ(I) over the interval I. $$ f \ \in \ C^n(I) $$

The function f(x) that satisfies a differential equation is known as a solution or an integral of the equation.

To solve a differential equation means to find all of its solutions - or at the very least, to understand their general behavior.

A solution to a differential equation is a function y(x) that belongs to class Cⁿ(I) on some interval I ∈ ℝ. That is, y(x) has continuous derivatives up to order n in I and satisfies the equation at every point x in that interval.

There are two main types of solutions:

• General solution (or general integral)
  This refers to the complete set of functions y(x) that satisfy the differential equation. In most cases, the general solution forms a family of functions of the type F(x) + c.

  Example. The differential equation $$ y' = 2x - 1 $$ has the following general solution: $$ y = x^2 + c $$ This represents an entire family of functions because the parameter c ∈ ℝ can take on any real value.

• Particular solution
  A particular solution is a single, specific function y(x) that satisfies the differential equation for a given constant c. The graph of each particular solution is referred to as an integral curve.

  Example. The differential equation $$ y' = 2x - 1 $$ has the particular solution: $$ y = x^2 + 1 $$ In this case, the constant c has been set to 1. So we have a single function, not a whole family. Another particular solution would be $$ y = x^2 + 2 $$ which corresponds to c = 2. Both are instances of the general solution y = x² + c. And so on.

Why do differential equations matter?

Differential equations are powerful tools for modeling situations where we don’t know the function explicitly, but we have information about how it behaves - such as its rate of change.

$$ u(x) = ? $$

This is especially common in physics and engineering.

For example, we might not know u(x), but we do know its rate of change with respect to x - namely, its first derivative u'(x):

$$ u'(x) $$

From this, we can determine the family of functions U(x) + k that share the same derivative, i.e., the same behavior or growth rate.

Note. For this reason, differential equations almost always have infinitely many solutions.

A hands-on example

Suppose we don’t know u(x), but we’re told that its rate of change is 2x:

$$ u'(x) = 2x $$

The family of functions that satisfy this condition is obtained by integrating u'(x):

$$ \int u'(x) \: dx = U(x) + k $$

In this case, the general solution of the differential equation is:

$$ \int 2x \: dx = x^2 + k $$

Where k is an arbitrary constant.

Because k can take on any real value, the differential equation has infinitely many solutions.

Note. The result is a family of functions U(x) + k, each distinguished by the value of the constant k. Since k is arbitrary, this family contains infinitely many distinct functions. However, they all share the same first derivative. Each individual function is called a particular solution of the differential equation. For example, u(x) = x² + 1 (where c = 1) is one particular solution. u(x) = x² + 2 (with c = 2) is another. And so on.

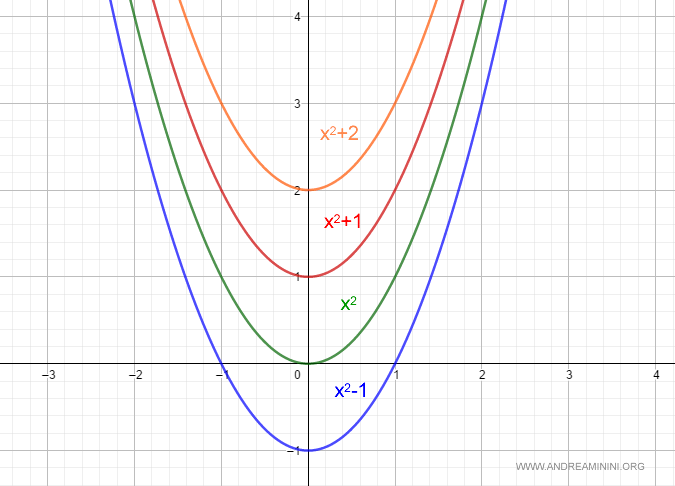
In general, a differential equation has infinitely many solutions, depending on a number of constants equal to the order of the equation.

In this example, there’s only one constant k because the equation is first-order.

$$ \int 2x \: dx = x^2 + k $$

Of course, not all differential equations are this straightforward.

Still, this simple case helps illustrate what differential equations are used for.

How can we check if a function solves a differential equation? While solving a differential equation may be tricky, checking a proposed solution is usually easy. Once you’ve found a candidate function u(x), you just compute its derivatives and substitute them into the equation. For example, we found that u = x² + k. Let’s differentiate and plug it into the original equation: $$ u'(x) = 2x $$ $$ D_x[ x^2 + k ] = 2x $$ $$ 2x + 0 = 2x $$ The identity holds, confirming that the solution is correct.

Example 2

Consider the differential equation:

$$ u'' = -u $$

We’re looking for a function whose second derivative is equal to the negative of the function itself.

Valid solutions include:

$$ u(x) = k \cdot \sin(x) \\ u(x) = k \cdot \cos(x) \\ u(x) = a \cdot \sin(x) + b \cdot \cos(x) \\ \vdots $$

We also have the trivial (constant) solution:

$$ u(x) = 0 $$

So the general solution includes infinitely many functions, possibly belonging to multiple distinct families.

Example 3

Let’s look at a more involved example to deepen the concept.

In this equation, the sum of the first derivative f′(x) and three times the second derivative f″(x) is equal to 9x:

$$ f'(x) + 3f''(x) = 9x $$

The problem is to determine the function f(x) that satisfies this equation.

Note. In this case, simply computing an integral won’t be enough. This equation is significantly more complex than the previous ones.

Explicit vs. Implicit Form

A differential equation is said to be in its explicit form (also called normal form) when the highest-order derivative \( y^{(n)} \) is isolated:

$$ y^{(n)} = f(x, y, y', ..., y^{(n-1)}) $$

Here, \( f \) is a real-valued function of \( n + 1 \) real variables, defined on \( \mathbb{R}^{n+1} \).

Alternatively, the equation can be written in its implicit form:

$$ F(x, y, y', ..., y^{(n)}) = 0 $$

In this case, \( F \) is a real-valued function of \( n + 2 \) variables defined on \( \mathbb{R}^{n+2} \), and the highest-order derivative is not explicitly isolated.

Order of a Differential Equation

The order (or degree) of a differential equation refers to the highest derivative that appears in the equation.

The highest-order derivative \( y^{(n)} \) determines the order of the equation.

The most common cases include:

• First-order differential equations
• Second-order differential equations
• Higher-order differential equations (third order or above)

Example 1

In the equation below, the highest derivative is the first derivative:

$$ f'(x) + 9x = 5 $$

This is a first-order differential equation.

Example 2

In this case, the second derivative appears as the highest-order term:

$$ f'(x) + 3f''(x) + 9x = 5 $$

This is a second-order differential equation.

Homogeneous, Nonhomogeneous, and Normal Form Equations

A differential equation can also be classified based on its structure:

• Homogeneous
  if the equation equals zero: $$ F(x, y, y', ..., y^{(n)}) = 0 $$
• Nonhomogeneous
  if the equation includes a non-zero term: $$ F(x, y, y', ..., y^{(n)}) \ne 0 $$
• Normal form
  if it is explicitly solved for the highest-order derivative: $$ y^{(n)} = f(x, y, y', ..., y^{(k-1)}) $$

Types of Differential Equations

Beyond the order, differential equations are further classified based on other characteristics:

• Ordinary Differential Equations (ODEs)
  These involve derivatives with respect to a single real variable.
• Partial Differential Equations (PDEs)
  These involve partial derivatives of functions of two or more real variables, such as \( f(x, y) \).

  Example. A classic PDE: $$ \frac{d^2 u(x, y)}{dx^2} + \frac{d^2 u(x, y)}{dy^2} = 0 $$

Another important distinction is between:

• Linear differential equations
  where all occurrences of the unknown function and its derivatives appear linearly.
• Nonlinear differential equations
  where the unknown function or its derivatives appear in nonlinear terms.

  Example. A nonlinear first-order equation: $$ y' = y^2 $$

How to Solve a Differential Equation

There is no universal method for solving all differential equations. Different types of equations require different techniques.

First-order differential equations

These are equations where the first derivative is the highest order that appears.

• Basic first-order equations
• Separable equations
• Linear first-order equations

Second-order differential equations

These equations include second derivatives as the highest-order term.

• Basic second-order equations
• Homogeneous linear second-order equations
• Complete (nonhomogeneous) second-order linear equations
• Equations without the unknown function y

And so on.