Cauchy Problem

Understanding the Cauchy Problem

The Cauchy problem involves finding a particular solution to a differential equation for a function $ y = f(x) $, where the corresponding integral curve passes through a given point $ (x_0, y_0) $: $$ \begin{cases} y' = F(x, y) \\ y_0 = f(x_0) \end{cases} $$

The condition $ y_0 = f(x_0) $ is known as the problem’s initial condition.

To solve a Cauchy problem, we must select - among the infinitely many solutions to the differential equation - the one that satisfies the prescribed initial condition.

In other words, we are looking for a function $ y = f(x) $ that both solves the differential equation and passes through the point $ (x_0, y_0) $.

Note. A Cauchy problem may involve one or more initial conditions. In general, the Cauchy problem for an $ n $th-order differential equation consists of the equation itself along with $ n $ conditions specified at the same point $ x_0 $, where $ x_0 \in I $ and $ y_0, y_1, \dots, y_{n-1} $ are the values assigned to $ y, y', y'', \dots, y^{(n-1)} $: $$ \begin{cases} y^{(n)} = f(x, y(x), \dots, y^{(n-1)}(x)) \\ y(x_0) = y_0 \\ y'(x_0) = y_1 \\ \vdots \\ y^{(n-1)}(x_0) = y_{n-1} \end{cases} $$ A function $ y \in C^n(I) $ is a solution to the Cauchy problem if it satisfies the differential equation at every point $ x \in I $ and fulfills all $ n $ initial conditions. Here, $ C^n(I) $ denotes the set of functions that are $ n $-times differentiable on the interval $ I $.

The number of initial conditions must match the number of arbitrary constants in the general solution. Furthermore, all initial values must be specified at the same point $ x_0 $.

A Practical Example

Consider the following first-order Cauchy problem:

$$ \begin{cases} y' - 2x = 3 \\ f(2) = 3 \end{cases} $$

Rewriting the equation explicitly:

$$ y' = 3 + 2x $$

We integrate to find the general solution:

$$ \int y' \, dx = \int (3 + 2x) \, dx $$

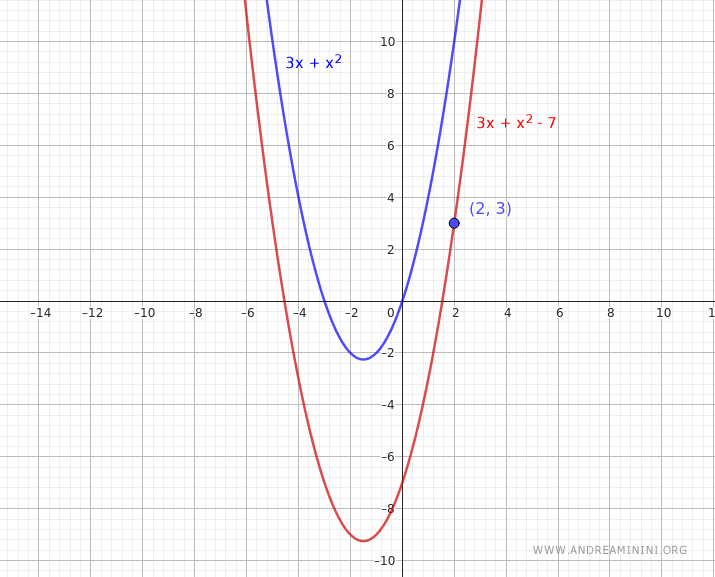
$$ y = 3x + x^2 + c $$

Now we apply the initial condition $ y(2) = 3 $:

$$ 3 = 3 \cdot 2 + 2^2 + c $$

$$ 3 = 6 + 4 + c $$

Solving for $ c $:

$$ c = -7 $$

Thus, the particular solution is:

$$ y = 3x + x^2 - 7 $$

This solution satisfies the initial condition and passes through the point $ (2, 3) $.

Graph showing the particular solution to the differential equation

Example 2

Now consider a simpler first-order equation:

$$ \begin{cases} y' = -e^{-x} \\ y(0) = 3 \end{cases} $$

Integrating the right-hand side:

$$ y = \int -e^{-x} \, dx = e^{-x} + c $$

Applying the initial condition $ y(0) = 3 $:

$$ 3 = 1 + c \Rightarrow c = 2 $$

The particular solution is:

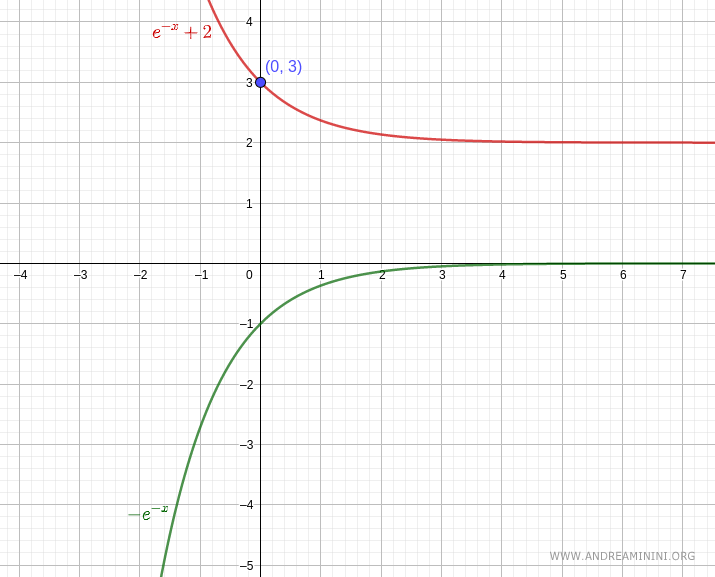
$$ y = e^{-x} + 2 $$

which passes through the point $ (0, 3) $.

Graph of the integral curve of the solution

Example 3

Now let’s look at a second-order case:

$$ \begin{cases} y'' = 2x \\ y'(1) = 2 \\ y(1) = 3 \end{cases} $$

There are two initial conditions, so we expect the general solution to include two arbitrary constants.

First, integrate $ y'' $ to obtain $ y' $:

$$ y' = \int 2x \, dx = x^2 + c_1 $$

Next, integrate $ y' $ to find $ y $:

$$ y = \int (x^2 + c_1) \, dx = \frac{1}{3}x^3 + c_1 x + c_2 $$

This is the general solution of the second-order equation.

Apply $ y'(1) = 2 $ to solve for $ c_1 $:

$$ 2 = 1^2 + c_1 \Rightarrow c_1 = 1 $$

Substitute $ c_1 = 1 $ into the general solution and apply $ y(1) = 3 $ to solve for $ c_2 $:

$$ 3 = \frac{1}{3}(1)^3 + 1(1) + c_2 = \frac{4}{3} + c_2 $$

$$ c_2 = 3 - \frac{4}{3} = \frac{5}{3} $$

So the particular solution is:

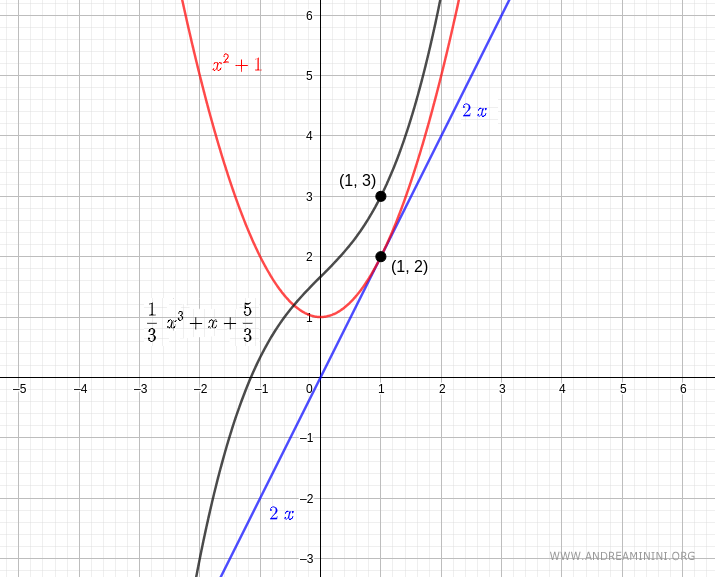
$$ y = \frac{1}{3}x^3 + x + \frac{5}{3} $$

This function satisfies both initial conditions:

$$ \begin{cases} y'' = 2x \\ y'(1) = 2 \\ y(1) = 3 \end{cases} $$

The first derivative $ y' = x^2 + 1 $ (shown in red) passes through the point $ (1, 2) $, while the solution $ y = \frac{1}{3}x^3 + x + \frac{5}{3} $ (in black) passes through $ (1, 3) $.

Graph showing both the solution and its first derivative

And so on.