Analyzing the Solution of a Differential Equation

Analyzing the solution \( y(t) \) of a differential equation is essential when the equation models a real-world phenomenon evolving over time \( t \), subject to a given initial condition.

In such models, time is the independent variable.

The analysis involves identifying the maximal interval of existence, the lifespan (both forward and backward in time), and the possible mode of breakdown of the solution.

Maximal Interval of Existence

The maximal interval of existence is the largest time interval over which the solution \( y(t) \) is defined and includes the initial time point.

Example

Consider the solution:

$$ y(t)= \frac{-2}{t^2 - 1} $$

with the initial condition:

$$ y(0) = 2 $$

The domain of the function is:

$$ (-\infty, -1) \cup (-1, 1) \cup (1, \infty) $$

Since the initial time \( t = 0 \) lies within the interval \( (-1, 1) \), this is the maximal interval of existence for the solution.

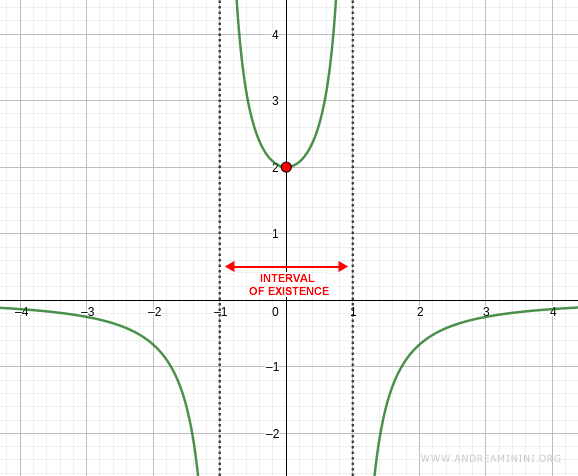
At \( t = 0 \), the function evaluates to \( y(0) = 2 \).

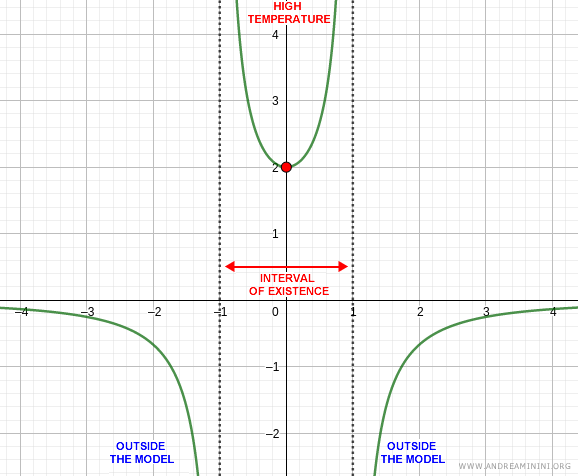
Outside the maximal interval, the mathematical solution exists, but it no longer corresponds to the physical reality modeled by the equation.

Example. As \( t \) approaches \( \pm 1 \), the solution diverges to infinity. Physically, this might represent a circuit overheating and failing due to excessive current. The behavior in the intervals \( (-\infty, -1) \) and \( (1, \infty) \) is of purely mathematical interest, with no real-world meaning. The model ceases to be valid beyond the interval \( (-1, 1) \).

Forward and Backward Lifespan

The forward and backward lifespan refer to the upper and lower bounds, respectively, of the interval of existence.

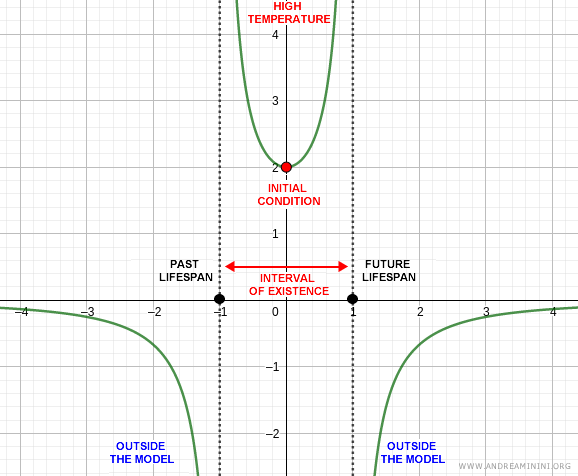
Note. In this example, the forward lifespan is 1, while the backward lifespan is -1.

Importantly, the lifespan depends on the initial condition - it is always measured relative to the point where the solution is initialized.

Types of Breakdown

Once the lifespan has been established, the next step is to assess whether the system experiences a breakdown as time progresses.

If the forward lifespan is infinite, the system persists indefinitely and remains well-defined for all future times.

If instead the forward lifespan is finite, the solution may encounter one of two types of breakdown:

• Blow-up
  This occurs when the solution diverges to \( +\infty \) or \( -\infty \) as \( t \) approaches the endpoint of the lifespan. For example, this could model a component in an electrical system overheating and failing due to sustained input.
• Breakdown
  This takes place when the solution \( y(t) \) causes the right-hand side of the differential equation to fall outside its domain of definition, effectively breaking the model.

Example

In the case below, the system exhibits a blow-up behavior:

In contrast, the following example shows a breakdown type of failure:

The system essentially collapses, ceasing to operate or produce any measurable effect.

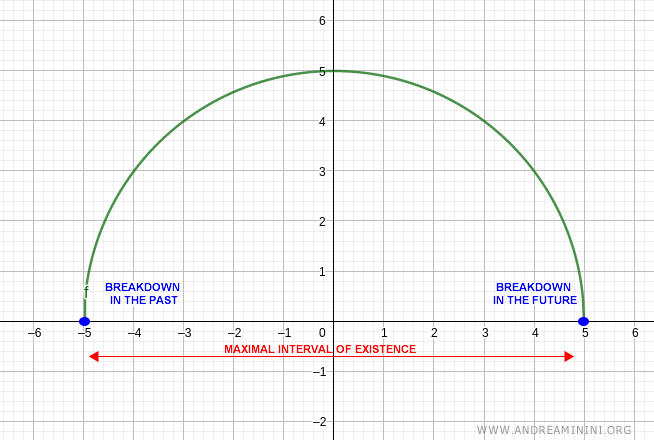
See this practical example.

And so on.