Differential Equations - Exercise 31

We are asked to solve the following first-order differential equation:

$$ \begin{cases} y'= \frac{-t}{y} \\ \\ y(0)=5 \end{cases} $$

This is a classic Cauchy problem.

The equation is separable and fits the form \( y' + a(t)b(y) = 0 \), where \( a(t) = 1 \) and \( b(y) = 1/y \). Such equations can be solved by separating variables.

Rewriting the derivative in Leibniz notation:

$$ \frac{dy}{dt} = \frac{-t}{y} $$

We now separate the variables:

$$ y \, dy = -t \, dt $$

Integrating both sides:

$$ \int y \, dy = \int -t \, dt $$

$$ \int y \, dy = - \int t \, dt $$

$$ \frac{y^2}{2} + C_1 = -\frac{t^2}{2} + C_2 $$

Multiplying both sides by 2:

$$ y^2 + 2C_1 = -t^2 + 2C_2 $$

Combining constants into a single constant \( C = 2C_2 - 2C_1 \):

$$ y^2 = -t^2 + C $$

Solving for \( y \):

$$ y = \pm \sqrt{C - t^2} $$

We determine the sign by applying the initial condition \( y(0) = 5 \):

$$ 5 = \pm \sqrt{C} \quad \Rightarrow \quad C = 25 $$

Hence, the particular solution to the Cauchy problem is:

$$ y = \sqrt{25 - t^2} $$

Verification. The derivative of the solution is: $$ y' = \frac{d}{dt} \left( \sqrt{25 - t^2} \right) = \frac{-t}{\sqrt{25 - t^2}} = \frac{-t}{y} $$ which confirms the solution satisfies the original equation.

Qualitative Analysis of the Solution

The maximal interval of existence for the solution is \( [-5, 5] \).

Here, 5 and -5 represent the forward and backward lifespans, respectively.

At \( t = 5 \), the solution breaks down, as the expression on the right-hand side of the differential equation becomes undefined.

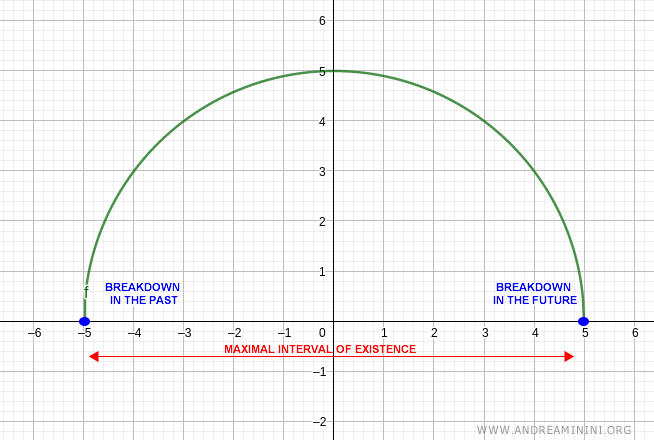
Note. The right-hand side of the equation is \( -t/y \), which is undefined when \( y = 0 \): $$ y' = \frac{-t}{y} \quad \Rightarrow \quad y' = \frac{-t}{0} $$ This singularity occurs precisely at \( t = 5 \), so the solution experiences a breakdown at that point.

Since the solution is an even function (symmetric with respect to \( t = 0 \)), the same breakdown also occurs at \( t = -5 \).

And so on.