Integral Calculus

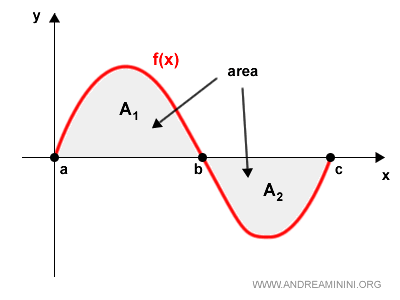
The integral is a fundamental concept in mathematical analysis, used to compute the area between the graph of a function and the x-axis.

Integral calculus was first employed by Archimedes and Eudoxus of Cnidus in the 4th century BCE, using what is now known as the method of exhaustion to approximate the area of irregular shapes.

The method is called "exhaustion" because it works by successively filling the area with regular polygons that increasingly approximate the target region.

How the method of exhaustion works

Suppose we want to calculate the area under a parabola over the interval [a, b].

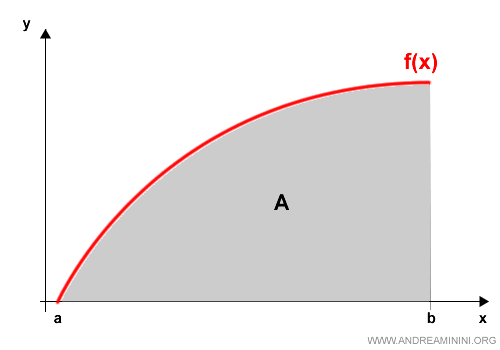
We begin by subdividing the area into inscribed polygons.

In this example, we use eight inscribed polygons: p₁, p₂, ..., p₈.

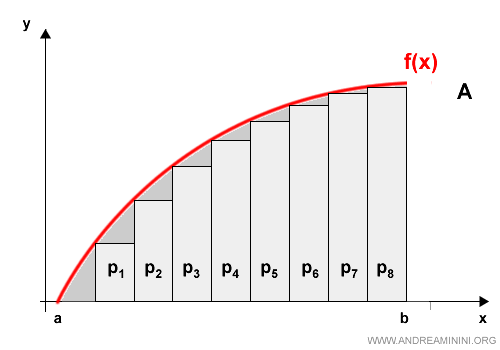
Calculating the area of these regular polygons is significantly more straightforward.

The sum of their areas, denoted A_min, provides a lower estimate of the area under the parabola.

$$ A_{min} = \sum_0^n A(p_n) $$

Next, we divide the region using circumscribed polygons.

These polygons lie entirely outside the parabola and enclose the region from above.

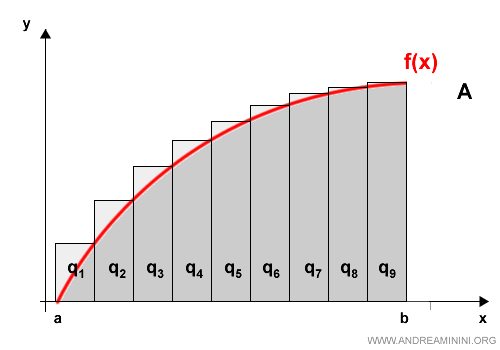
We then compute the total area of these n regular polygons, labeled from q₁ to q₉.

This yields an upper estimate, A_max, of the area under the parabola.

$$ A_{max} = \sum_0^n A(p_n) $$

The actual area, A, lies somewhere between these two estimates:

$$ A_{min} \le A \le A_{max} $$

Note. The accuracy of the estimate increases with the number of polygons used to approximate the area. As the number of regular polygons n approaches infinity, the gap between A_min and A_max narrows, and both estimates converge to the true area of the parabola. $$ \lim_{n \rightarrow \infty} A_{min} = \lim_{n \rightarrow \infty} A_{max} = A $$

The difference between definite and indefinite integrals

There are two main types of integrals:

• Definite integral
  This type of integral is evaluated over a specific interval (a, b). It is commonly used to compute the area under a curve, and the result is a real number. $$ \int_a^b f(x) \:\:dx $$
• Indefinite integral
  This integral is computed over the entire domain of the function. It represents the antiderivative of the function - that is, it reverses the process of differentiation. The result is not a single value, but a general expression: a family of functions. $$ \int f(x) \:\:dx $$

Note. Definite and indefinite integrals serve different purposes and follow distinct computational approaches. They should not be confused.

The Fundamental Theorem of Calculus

If a function is continuous on the interval [a, b], then the integral function $$ F(x) = \int_a^x f(t) \: dt $$ is differentiable, and its derivative is equal to the integrand: $$ D[F(x)] = f(x) $$

The function \( F(x) \) is referred to as an antiderivative (or primitive) of \( f(x) \).

This theorem establishes a fundamental connection between integration and differentiation.

A Practical Example

On the interval [0, x], the integral of the function \( 2t \) is given by:

$$ F(x) = \int_0^x 2t \: dt = x^2 $$

The integrand is:

$$ f(x) = 2x $$

The integral function is:

$$ F(x) = x^2 $$

The derivative of the integral function is:

$$ F'(x) = D[x^2] = 2x $$

Therefore, $$ F'(x) = f(x) $$ which confirms that the derivative of the integral function is equal to the original integrand evaluated at \( x \).

This result holds for any continuous function \( f(x) \) defined on a closed interval [a, b].

Proof and Explanation

To compute the derivative of the integral function, we evaluate the limit of the difference quotient as \( h \to 0 \):

$$ \lim_{h \to 0} \frac{F(x + h) - F(x)}{h} $$

$$ = \lim_{h \to 0} \frac{1}{h} \cdot \left[ \int_a^{x + h} f(t) \: dt - \int_a^x f(t) \: dt \right] $$

Using the additivity property of definite integrals, we can write:

$$ = \lim_{h \to 0} \frac{1}{h} \cdot \left[ \int_x^{x + h} f(t) \: dt \right] $$

Note: By the Mean Value Theorem for Integrals, since \( f(t) \) is continuous on [x, x + h], there exists a point \( x_0 \in [x, x + h] \) such that: $$ \int_x^{x + h} f(t) \: dt = f(x_0) \cdot h $$ Therefore, $$ \frac{1}{h} \cdot \int_x^{x + h} f(t) \: dt = f(x_0) $$ As \( h \to 0 \), the point \( x_0 \) lies within the shrinking interval [x, x + h], so: $$ \lim_{h \to 0} x_0 = x \quad \Rightarrow \quad \lim_{h \to 0} f(x_0) = f(x) $$

Thus, the derivative of the integral function is:

$$ F'(x) = f(x) $$

This completes the proof of the Fundamental Theorem of Calculus.

And so on.