Multiple Integrals

What Are Multiple Integrals?

Multiple integrals - such as double and triple integrals - are definite integrals of functions that depend on two or more variables (or dimensions). $$ \int f(x,y) \ dx \ dy $$ $$ \int f(x,y,z) \ dx \ dy \ dz $$

When a function involves two variables, the corresponding integral is called a double integral. If the function depends on three variables, we refer to it as a triple integral.

What Are They Used For?

A double integral allows us to compute the volume beneath a surface defined by a function of two variables, over a given region in the plane.

Note. Integrals over two or more variables retain the same fundamental properties as single-variable definite integrals.

Double Integral

The multiple integral of a function \( f(x, y) \) in two variables (i.e., over two dimensions) is called a double integral.

It is typically denoted using a double integral sign:

$$ \int f(x,y) \ dx \ dy = \iint f(x,y) \ dx \ dy $$

In a double integral, the region over which the function is defined is partitioned into small rectangles, whose contributions are summed.

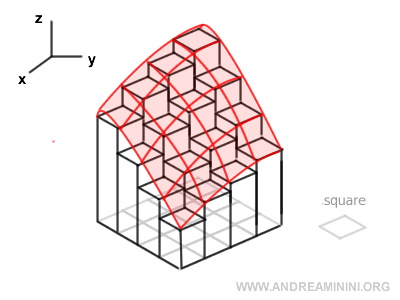
The value of the integral is the limit of this sum as the area of each rectangle approaches zero.

Triple Integral

The multiple integral of a function \( f(x, y, z) \) in three variables (i.e., over three dimensions) is called a triple integral.

It is commonly written using a triple integral sign:

$$ \int f(x,y,z) \ dx \ dy \ dz = \iiint f(x,y,z) \ dx \ dy \ dz $$

In a triple integral, the domain is subdivided into tiny cubes, and the function values over these cubes are summed.

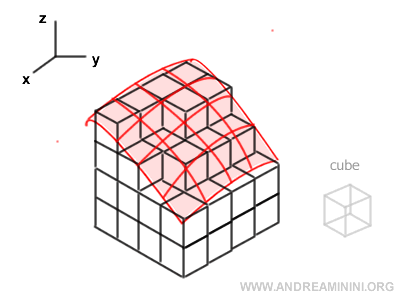
The integral corresponds to the limit of this sum as the volume of each cube becomes infinitesimally small.

And so on.