Permutations

A permutation is a one-to-one correspondence of a set with itself. Any set containing n elements admits exactly n! (n factorial) distinct permutations. $$ n! = n \cdot (n-1) \cdot (n-2) \cdot \cdot \cdot 3 \cdot 2 \cdot 1 $$ The notation n! is read as “n factorial” and is defined for all $ n > 1 $.

A simple way to think about permutations is to view them as all possible orderings of n distinct elements. Every ordering is counted, and two permutations differ whenever the arrangement of the elements changes in any position.

The total number of simple permutations of a set with n elements is

$$ P_n = n! = n \cdot (n-1) \cdot ... \cdot 2 \cdot 1 $$

By convention, when n equals 0, we define $ 0! = 1 $.

It is essential to keep in mind that a simple permutation uses every element of the set exactly once. No element may be repeated and none may be left out.

Example. How many different words can be formed using the letters A, B, C exactly once? Since $ n! = 3 \cdot 2 \cdot 1 = 6 $, there are six permutations: $$ ABC, ACB, BAC, BCA, CAB, CBA $$ Each permutation includes all three letters, each occupying a unique position.

When a set contains repeated elements, the count changes. In this case, we use the formula for permutations with repetition:

$$ P_n^{(h,k,..)} = \frac{ n! }{ h! k! ... } $$

Example. Consider the word “ANNA”. It contains four letters, so the number of possible arrangements is $$ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24. $$ If all four letters were distinct, we would obtain 24 different words. But because ANNA contains repeated letters, many arrangements coincide. The long list in the example makes the repetitions evident, with several occurrences of “ANNA”, “ANAN”, “AANN”, and similar patterns.

From the complete set of 24 arrangements, only 6 are truly distinct. The reason is straightforward: swapping identical letters does not produce a new configuration. To count only the unique outcomes, we apply the formula for permutations with repetition. In ANNA, the letter A appears twice ($ h = 2 $) and N also appears twice ($ k = 2 $). Therefore, $$ P_n^{(h,k,..)} = \frac{4!}{2! \cdot 2!} = \frac{24}{4} = 6. $$ Thus, the six distinct permutations obtained from ANNA are:

ANNA, ANAN, AANN, NANA, NAAN, NNAA.

A practical example

Let us consider a set X with five elements:

$$ X = \{ a,b,c,d,e \} $$

Here are a few of its permutations:

$$ a,b,c,d,e \\ b,a,c,d,e \\ c,d,b,a,e \\ e,a,c,b,d \\ \vdots $$

Each permutation represents a specific one-to-one correspondence between the elements of X.

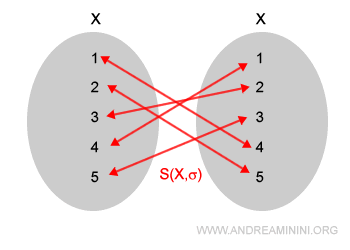
Note. The collection of all permutations of X is denoted S(X). Each element of S(X) can be viewed as a composition of mappings describing a particular rearrangement. Together with composition σ, S(X) forms an algebraic structure known as a group.

The set A has cardinality 5, because it contains five elements:

$$ n = 5 $$

This means that A has one hundred and twenty distinct permutations:

$$ 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 $$

In this case n! is equal to 120.

Representing Permutations

There are several standard ways to represent permutations of a set X, each suited to a different level of abstraction or computational convenience.

As a first step, any finite set X with n elements can be relabelled using the integers from 1 to n. This relabelling alters nothing about the underlying structure of the permutation; it simply streamlines the notation.

For example, if $$ X = \{ a,b,c,d,e \}, $$ we may adopt the equivalent representation $$ X = \{ 1,2,3,4,5 \}. $$

Note. In algebra, any finite set with n elements is canonically identified with \( \{1,2,\dots,n\} \). The nature of the elements themselves is irrelevant; what matters is the structure of the mappings acting on them.

Two-line notation

A classical representation of a permutation \( p \colon X \to X \) is the two-line notation:

$$ p = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ i_1 & i_2 & i_3 & i_4 & i_5 \end{pmatrix}. $$

The first line lists the elements of X in increasing order. The second line gives their images under the permutation.

For example:

$$ p_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \end{pmatrix}. $$

Thus, \( p_1(1)=2 \), \( p_1(2)=3 \), \( p_1(3)=1 \), \( p_1(4)=5 \), \( p_1(5)=4 \). With five elements, the total number of permutations is $$ 5! = 120. $$

A second example is:

$$ p_2 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 5 & 3 & 1 \end{pmatrix}. $$

Since the top row is invariably the natural ordering \( 1,\dots,n \), it is customary to omit it.

One-line notation

In one-line notation, a permutation is recorded by listing only the second row:

$$ p_1 = (2,3,1,5,4), \qquad p_2 = (4,2,5,3,1). $$

Here the position of each entry determines the argument of the permutation. For instance, in \( p_1 = (2,3,1,5,4) \), the first entry 2 signifies \( p_1(1)=2 \), the second entry 3 signifies \( p_1(2)=3 \), and so forth.

Explicitly:

$$ p_1 : X \to X $$ $$ 1 \mapsto 2 $$ $$ 2 \mapsto 3 $$ $$ 3 \mapsto 1 $$ $$ 4 \mapsto 5 $$ $$ 5 \mapsto 4 $$

and

$$ p_2 : X \to X $$ $$ 1 \mapsto 4 $$ $$ 2 \mapsto 2 $$ $$ 3 \mapsto 5 $$ $$ 4 \mapsto 3 $$ $$ 5 \mapsto 1 $$

Cycle notation

In abstract algebra, the most concise and conceptually illuminating format is the cycle notation. It captures the essential structure of the permutation by grouping together the points that move among themselves.

Definition. Cycle. A cycle \( (x_1\,x_2\,\dots\,x_m) \) denotes the mapping \( x_1 \mapsto x_2 \), \( x_2 \mapsto x_3 \), …, \( x_m \mapsto x_1 \). Two cycles are disjoint if they involve disjoint subsets of X.

For instance, the permutation \( p_1 = (2,3,1,5,4) \) decomposes into the disjoint cycles:

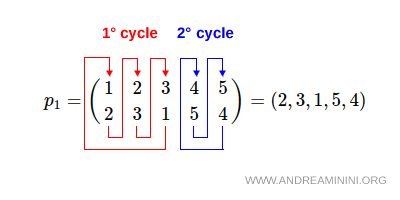
The first cycle is $$ (1,2,3), $$ and the second is $$ (4,5). $$

Thus,

$$ p_1 = (1,2,3)(4,5). $$

Equivalently:

$$ p_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \end{pmatrix} = (2,3,1,5,4) = (1,2,3)(4,5). $$

Note. Cycle notation displays only the nontrivial action of the permutation; elements fixed by the permutation do not appear.

The permutation \( p_2 = (4,2,5,3,1) \) decomposes as follows:

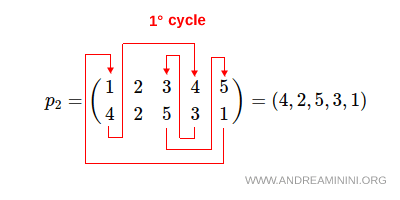
Its cycle structure is

$$ (1,4,3,5), $$

while 2 is a fixed point and is therefore omitted. Hence,

$$ p_2 = (1,4,3,5). $$

Decomposition into transpositions

Each cycle can be further decomposed into a product of transpositions, which are 2-cycles. This decomposition forms the basis for studying the parity of permutations.

The standard identity is:

$$ (x_1\,x_2\,\dots\,x_m) = (x_1\,x_m)(x_1\,x_{m-1})\dots(x_1\,x_3)(x_1\,x_2). $$

Definition. Transposition. A transposition is a cycle of length two, i.e. a swap of two elements.

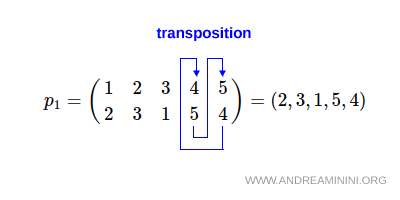
For example, $$ (1,2,3) = (1,3)(1,2). $$ The cycle (4,5) is itself a transposition.

Hence the permutation \( p_1 \) can be written as:

$$ p_1 = (1,2,3)(4,5) = (1,3)(1,2)(4,5). $$

Parity of a permutation

The number of transpositions in such a decomposition determines the parity of the permutation, a fundamental concept in group theory:

• Even permutation: expressible as a product of an even number of transpositions.
• Odd permutation: expressible as a product of an odd number of transpositions.

Since \( p_1 = (1,3)(1,2)(4,5) \) consists of three transpositions, it is an odd permutation.

How to Generate All Permutations

To systematically list all permutations of a finite set, we apply the enumeration principle. This allows us to construct every possible arrangement in an ordered and complete way.

Method 1

Consider a set with four elements:

S = {1,2,3,4}

The total number of permutations is

$$ 4! = 24. $$

We divide 24 by the number of elements \( n = 4 \), obtaining \( 24/4 = 6 \). This tells us that exactly six permutations begin with each of the four elements. We therefore start by writing the first element six times:

1
1
1
1
1
1

We still have \( n-1 = 3 \) elements to arrange, namely 2, 3, and 4. We distribute them in the second position in pairs, following increasing order:

1,2
1,2
1,3
1,3
1,4
1,4

Next, we fill the third position by inserting the missing element in each tuple, again following increasing order:

1,2,3
1,2,4
1,3,2
1,3,4
1,4,2
1,4,3

Note. For a partial tuple such as (1,2), the missing elements are 3 and 4. Following ascending order, we insert 3 first and then 4.

Finally, we complete each tuple by inserting the last missing element:

1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2

We now repeat the same procedure starting with 2:

2,1,3,4
2,1,4,3
2,3,1,4
2,3,4,1
2,4,1,3
2,4,3,1

Then starting with 3:

3,1,2,4
3,1,4,2
3,2,1,4
3,2,4,1
3,4,1,2
3,4,2,1

Finally, starting with 4:

4,1,2,3
4,1,3,2
4,2,1,3
4,2,3,1
4,3,1,2
4,3,2,1

We now combine all four groups into a single list and obtain the complete set of 24 permutations of {1,2,3,4}:

1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2
2,1,3,4
2,1,4,3
2,3,1,4
2,3,4,1
2,4,1,3
2,4,3,1
3,1,2,4
3,1,4,2
3,2,1,4
3,2,4,1
3,4,1,2
3,4,2,1
4,1,2,3
4,1,3,2
4,2,1,3
4,2,3,1
4,3,1,2
4,3,2,1

Method 2

We again consider the set

S = {1,2,3,4}

which has 24 permutations in total.

As before, we compute \( 24/4 = 6 \) and write the first element six times:

1
1
1
1
1
1

Now we write the sequence 2,3,4 vertically in the second position:

1,2
1,3
1,4
1,2
1,3
1,4

We now cyclically shift the sequence from 2,3,4 to 3,4,2 and write it again in the third position:

1,2,3
1,3,4
1,4,2
1,2,3
1,3,4
1,4,2

We perform another cyclic shift, obtaining 4,2,3, and add it as the fourth position:

1,2,3,4
1,3,4,2
1,4,2,3
1,2,3,4
1,3,4,2
1,4,2,3

Note. From the second column onwards, the entries align diagonally. This structural regularity makes the table easier to construct mechanically. Once the first two columns are written, the remaining ones follow automatically.

We repeat the procedure with 2 in the first position:

2,1,3,4
2,3,4,1
2,4,1,3
2,1,3,4
2,3,4,1
2,4,1,3

Then with 3:

3,1,2,4
3,2,4,1
3,4,1,2
3,1,2,4
3,2,4,1
3,4,1,2

Then with 4:

4,1,2,3
4,2,3,1
4,3,1,2
4,1,2,3
4,2,3,1
4,3,1,2

Combining the four groups yields the complete list of all 24 permutations of {1,2,3,4}.

The final result is identical to that of Method 1. Both procedures produce the full set of permutations in a systematic and fully determined manner.