Prime Numbers

What Are Prime Numbers?

A prime number is an integer greater than 1 that can only be divided by 1 and itself.

In other words, a prime number has exactly two distinct factors: 1 and itself.

Here are some examples of prime numbers:

$$2 \ , \ 3 \ , \ 5 \ , \ 7 \ , \ 11 \ , \ 13 \ , \ 17 \ , \ 19 \ , \ 23 \ , \ 29 \ , \ 31 \ ...$$

For instance, the number 7 has only two factors: 1 and 7.

$$7 \div 1 = 7$$

$$7 \div 7 = 1$$

Since no other numbers divide 7 evenly, it is a prime number.

Why isn't 1 considered a prime number? Because it has only one factor: itself. If 1 were classified as prime, the unique prime factorization of numbers would no longer hold, contradicting the fundamental theorem of arithmetic.

An Alternative Definition

Another way to define a prime number is:

An integer $a$ is a prime number if, whenever it divides a product $bc$ (where $b$ and $c$ are integers), it must also divide at least one of the factors. $$\forall a|bc \rightarrow a|b \lor a|c$$

For example, let’s take $a = 3$, a prime number, and check this property using a product $bc$.

If we choose $b = 6$ and $c = 5$, then $bc = 6 \times 5 = 30$.

Here, $a = 3$ divides $bc = 30$, and it also divides at least one of the factors ($b = 6$), confirming the definition.

How many prime numbers are there? Infinitely many! This was first proven by Euclid. The largest known prime number, discovered in 2018, is $2^{82,589,933} - 1$, which has over 24 million digits.

One of the most efficient ways to identify prime numbers up to $N$ is the Sieve of Eratosthenes.

Prime Factorization

Any composite number can be expressed as a product of prime numbers.

Example

The number 30 is not prime.

Its prime factorization is:

$$30 = 2 \cdot 3 \cdot 5$$

Since 30 is divisible by 2, 3, and 5 (as well as by 1 and itself), it is not a prime number.

The Fundamental Theorem of Arithmetic

According to the fundamental theorem of arithmetic:

Every integer greater than 1 has a unique prime factorization, meaning it can be expressed as a product of distinct irreducible elements, each raised to a positive exponent $e_k > 0$. $$n=f_1^{e_1} \cdot f_2^{e_2} ... f_k^{e_k}$$

For example, consider $n = 180$.

Its prime factorization is:

$$180 = 2^2 \cdot 3^2 \cdot 5^1$$

Here, 2, 3, and 5 are prime numbers, and their respective exponents $e_1 = 2$, $e_2 = 2$, and $e_3 = 1$ are positive.

Thus, we can express $n = 180$ as:

$$n = f_1^{e_1} \cdot f_2^{e_2} \cdot f_3^{e_3} = 2^2 \cdot 3^2 \cdot 5^1$$

The factorization is unique, except for the order of the factors.

$$180 =  2^2 \cdot 3^2 \cdot 5^1$$

This confirms the fundamental theorem of arithmetic.

The same rule applies to any integer greater than 1.

Note: Changing the order of the factors does not affect the uniqueness of the factorization, as the prime factors remain the same. $$180 =  2^2 \cdot 3^2 \cdot 5^1 = 3^2 \cdot 5^1 \cdot 2^2 =  5^1 \cdot 2^2 \cdot 3^2$$

Prime Number Theorem

The ratio $p(x) / (x / \log x)$ approaches 1 as $x$ grows indefinitely: $$\lim_{x \rightarrow \infty} \frac{p(x)}{\frac{x}{\log x}} = 1$$ where $x$ is a real number with $x > 0$, and $p(x)$ represents the number of prime numbers less than $x$.

In other words, the probability that a randomly chosen integer $n$ is prime is approximately $1 / \log n$.

Gauss was the first to observe that the distribution of prime numbers closely follows the function $x / \log x$ asymptotically.

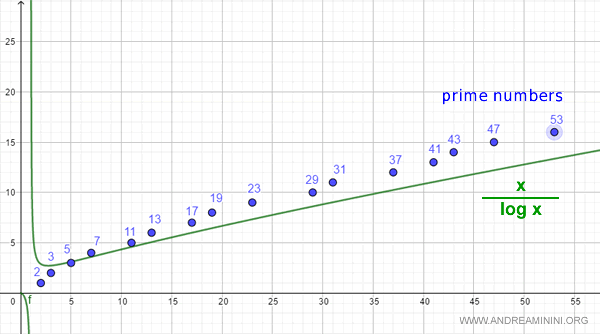
This function, $x / \log x$, provides a useful estimate of how many prime numbers exist below a given number $n$.

Example. Let’s estimate the number of primes below $n = 55$ using Gauss’s formula: $$\frac{n}{\log n} = \frac{55}{\log 55} = 13.72$$ The estimate suggests there are about 14 primes below 55. In reality, counting them gives 16, but the approximation is fairly accurate. This formula becomes increasingly useful for large values of $n$.

From this, we can approximate the probability that an integer $n$ is prime:

$$\frac{1}{\log n}$$

This also implies that, on average, we would expect to check about $\log n$ numbers before finding a prime greater than $n$.

$$\log n$$

Example. Suppose we want to find the next prime after $n = 43$. $$\log 43 = 3.76$$ The estimate suggests we should find a prime in about 4 attempts. $$44 \text{ (Attempt 1) } \\ 45 \text{ (Attempt 2) } \\ 46 \text{ (Attempt 3) } \\ 47 \text{ (Prime - Attempt 4) }$$ As expected, the next prime, 47, was found in 4 steps. While this formula is only an approximation, it provides a reasonable expectation for the number of trials needed. This property is particularly valuable in cryptography.

Mersenne Prime Numbers

Mersenne numbers are integers of the form:

$$M_n = 2^n - 1$$

where $n$ is a positive integer.

Not all Mersenne numbers are prime—only certain values of $n$ produce a prime $M_n$.

For example:

- $M_2 = 2^2 - 1 = 3$ (prime)
- $M_3 = 2^3 - 1 = 7$ (prime)
- $M_4 = 2^4 - 1 = 15$ (not prime)
- $M_5 = 2^5 - 1 = 31$ (prime)

Mersenne numbers exhibit an interesting property: if $M_n = 2^n - 1$ is prime, then $n$ must also be prime.

However, the converse is not necessarily true: just because $n$ is prime does not guarantee that $M_n$ is also prime. For instance, $n = 11$ is prime, but $M_{11} = 2^{11} - 1 = 2047$, which is not prime (since $2047 = 23 \times 89$).

This property makes Mersenne numbers particularly useful in the search for large prime numbers.

Rather than testing $2^n - 1$ for every $n$, we only check values where $n$ is prime, significantly reducing the number of computations.

Strategy for Finding Mersenne Primes

1. Select a prime number $n$.
2. Compute the corresponding Mersenne number $M_n = 2^n - 1$.
3. Perform a primality test to determine whether $M_n$ is actually prime.

This method has led to the discovery of the largest known prime numbers.

However, while limiting the search to prime values of $n$ reduces the number of candidates, each $M_n$ must still undergo a primality test, which remains computationally intensive.

Note. It’s worth emphasizing that not all prime numbers are Mersenne primes, and not all Mersenne numbers are prime.

Additional Notes

Here are a few additional insights on prime numbers:

• Difference Between Prime and Irreducible Numbers
  In the set of integers, prime numbers and irreducible numbers coincide. However, in other algebraic structures, prime elements do not always correspond to irreducible elements.
• Irrationality of Prime Square Roots
  The square root of a prime number is always irrational.

And so on.