Quark Confinement

Quark confinement is the phenomenon that prevents quarks from ever existing in isolation: they are always locked inside composite particles. Unlike most forces, the strong interaction becomes stronger as quarks are pulled farther apart, which makes it impossible to separate them.

This counterintuitive behavior is a defining feature of quantum chromodynamics (QCD), the theory that governs the strong nuclear force.

In nature, quarks are never found on their own. They are permanently trapped inside composite particles known as hadrons-such as protons and neutrons, the fundamental building blocks of atomic nuclei.

The force responsible for confinement is the strong interaction, mediated by gluons, the gauge bosons of QCD.

Note. Unlike photons in quantum electrodynamics (QED), gluons themselves carry color charge and can interact with one another. This self-coupling property makes QCD a non-Abelian and highly non-linear theory.

The strong force binds protons and neutrons together inside the atomic nucleus, overcoming the electrostatic repulsion between their positive charges. This binding is what makes matter stable.

One of the most remarkable aspects of the strong interaction is its counterintuitive dependence on distance between quarks:

• At extremely short distances (corresponding to very high energies), the strong force weakens, and quarks behave almost like free particles. This phenomenon is known as asymptotic freedom, and it has been confirmed through high-energy collision experiments.
• At larger separations, however, the force grows stronger, as if the quarks were connected by an elastic band. Instead of fading with distance, the interaction intensifies. When two quarks are pulled apart, the force increases with distance \( r \), much like the tension in a stretched spring. The system’s potential energy then rises linearly with separation: $$ V(r) \approx \sigma \cdot r $$ where \( \sigma \) is the string tension, approximately \( 0.2 \,\text{GeV}^2 \).

Note. Confinement can be overcome only under extreme conditions, such as the ultra-high temperatures of the early universe or during high-energy collisions at the LHC, where a quark-gluon plasma can briefly form.

What happens if you try to pull two quarks apart?

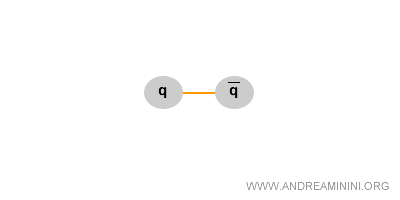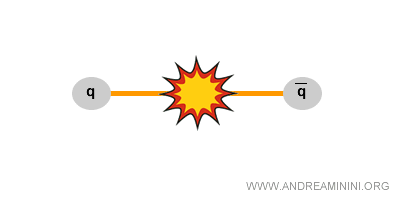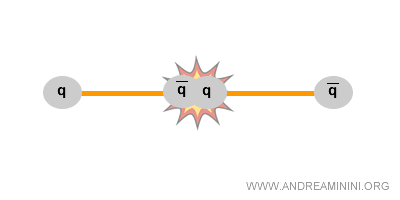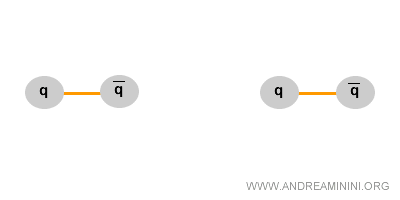
When you attempt to separate two quarks, the color field between them stores an ever-increasing amount of energy.

Once this energy surpasses a critical threshold, it is converted into mass according to \( E = mc^2 \), leading to the spontaneous creation of new quark-antiquark pairs from the vacuum.

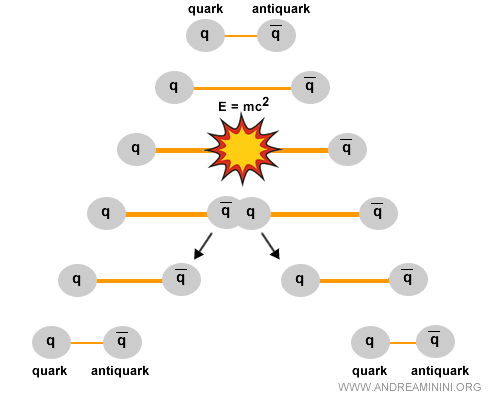
This happens because the energy required to separate quarks is greater than the energy needed to generate fresh particles.

As a consequence, the process never yields a free quark. Instead, new hadrons are produced.

This is why no free quark has ever been observed.

Why can’t a single quark exist?

A solitary quark cannot exist because confinement requires every particle to be color-neutral.

• Baryons (such as the proton) are composed of three quarks, each carrying a different color charge-red, green, and blue. Together they combine into a neutral state, commonly described as “white.”
• Mesons, on the other hand, consist of a quark paired with its corresponding antiquark. The quark’s color is exactly canceled by the antiquark’s anti-color.
  

In both cases, the end result is always a color-neutral system.

The three fundamental colors-red, green, and blue-combine in baryons, while the three anti-colors-anti-red, anti-green, and anti-blue-combine in antibaryons. In both situations, the outcome is a perfectly neutral “white” state, with no net color charge.

The same rule applies to mesons: the color of a quark is always precisely balanced by the anti-color of its antiquark partner.

For this reason, a free quark can never exist: on its own, it cannot achieve color neutrality. Put simply, there is no such thing in nature as a “white quark”.

Whenever a quark is pulled away, it instantly recombines with other quarks or antiquarks, giving rise to new color-neutral hadrons.

Note. Although confinement is firmly supported by experimental evidence, a complete mathematical proof is still lacking. Establishing such a proof remains one of the Millennium Prize Problems posed by the Clay Mathematics Institute, which has offered a one-million-dollar reward for its solution. Future research on quark-gluon plasma and non-perturbative methods may eventually provide a definitive explanation.

And the exploration continues…