Nonnegative integers

The nonnegative integers are defined as the set obtained by adjoining zero to the natural numbers. This set is denoted by N₀. $$ N_0 = N \cup \{ 0 \} $$

It consists of all integers that are greater than or equal to zero.

$$ N_0 = \{ \ 0 \ , \ 1 \ , \ 2 \ , \ 3 \ , \ ... \ \} $$

The set of nonnegative integers N₀ contains the set of natural numbers N.

$$ N_0 ⊂ N $$

Consequently, the set N₀ satisfies the five axioms of the natural numbers.

The natural numbers are closed under addition and multiplication
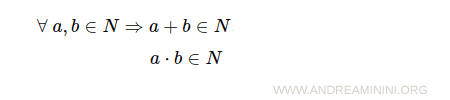
Commutative property of addition and multiplication
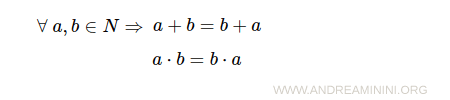
Associative property of addition and multiplication
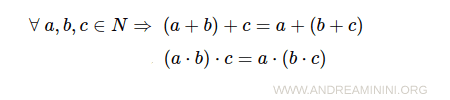
Distributive property of multiplication over addition
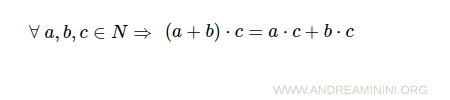
Existence of a multiplicative identity

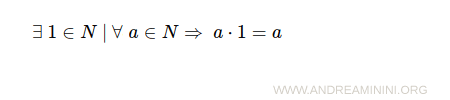
To fully characterize the set of nonnegative integers, one additional axiom is required.

Axiom of the additive identity.
Adding zero to any nonnegative integer leaves the number unchanged. $$ \exists \ 0 \in N_0 \ | \ \forall \ a \in N_0 \Rightarrow a+0=a $$
Example. The sum 5+0 equals 5. $$ 5+0 = 5 $$

Useful observations

Some useful remarks concerning the nonnegative integers.

The additive identity is zero
Every nonnegative integer added to zero remains unchanged. $$ \forall \ a \in N_0 \Rightarrow a + 0 = a $$
The additive identity is unique
No element other than zero serves as an additive identity.
Proof. We establish the uniqueness of the additive identity by contradiction. There are two possible cases:

1) the additive identity is unique
2) the additive identity is not unique

Assume that there exists a second additive identity ε, distinct from zero. Then the condition $$ \exists \ \epsilon \in N_0 \ | \ \forall \ a \in N_0 \Rightarrow a + \epsilon = a $$ would hold, together with $$ \exists \ 0 \in N_0 \ | \ \forall \ a \in N_0 \Rightarrow a + 0 = a $$ Since both are assumed to be additive identities, adding zero to any element of N yields the same element: $$ a+0=a $$ Similarly, adding ε to any element of N also yields the same element: $$ a+ \epsilon = a $$ Now consider a=ε and add zero: $$ a+0=\epsilon + 0 = \epsilon $$ Next, consider a=0 and add ε: $$ a+\epsilon = 0 + \epsilon = 0 $$ By the commutative property of addition for the natural numbers, x+y=y+x, and therefore $$ \epsilon + 0 = 0 + \epsilon $$ Since ε+0=ε and 0+ε=0, it follows that $$ \underbrace{ \epsilon + 0 }_{\epsilon} = \underbrace{0 + \epsilon}_0 $$ which implies $$ \epsilon = 0 $$ Hence ε coincides with zero. Therefore, in the set of nonnegative integers N₀, zero is the unique additive identity. This completes the proof.
Any nonnegative integer multiplied by zero equals zero $$ \forall \ a \in N_0 \Rightarrow a \cdot 0 = 0 $$
Proof. By the fifth axiom of the natural numbers, multiplying any natural number by 1 leaves it unchanged, since 1 is the multiplicative identity. $$ a = a \cdot 1 $$ Using the sixth axiom for N₀, we rewrite 1 as 1+0. $$ a = a \cdot 1 = a \cdot (1 + 0) $$ Applying the distributive property (fourth axiom), we obtain $$ a = a \cdot 1 = a \cdot (1 + 0) = a \cdot 1 + a \cdot 0 $$ Since 1 is the multiplicative identity (fifth axiom), we have a·1=a. $$ a = a \cdot 1 = a \cdot (1 + 0) = a \cdot 1 + a \cdot 0 = a + a \cdot 0 $$ This yields $$ a = a + a \cdot 0 $$ For the equality a=a to hold, the term a·0 must act as the additive identity. $$ a = a+\underbrace{a \cdot 0}_0 $$ Because the additive identity is unique and equal to zero, it follows that $$ a \cdot 0 = 0 $$ Therefore, any nonnegative integer multiplied by zero is equal to zero. $$ \forall \ a \in N_0 \Rightarrow a \cdot 0 = 0 $$

And so on.