Sets of numbers

In mathematics, numbers are organized into different sets, each one designed to capture specific properties and extend what we can describe and compute. The main sets of numbers are the following:

• Set of natural numbers (N)
  This set includes the positive integers used for counting objects and quantities. It is the oldest and most intuitive number system, rooted in everyday experience.

  Set of natural numbers including zero N₀
  This variant of the natural numbers also includes zero, allowing the representation of empty quantities.

• Set of integers (Z)
  The set of integers extends the natural numbers by including negative values and zero. It allows us to describe gains and losses, directions, and differences. The natural numbers form a subset of this set.
• Set of rational numbers (Q)
  Rational numbers are those that can be written as the ratio of two integers with a nonzero denominator. They include fractions and decimal numbers with finite or repeating expansions. All integers belong to this set.
• Set of irrational numbers (I)
  This set contains real numbers that cannot be expressed as a ratio of two integers. Their decimal expansions are infinite and non-repeating. Irrational numbers are completely distinct from rational numbers.
• Set of real numbers (R)
  The real numbers are obtained by combining rational and irrational numbers. Together, they form a continuous set that corresponds to all points on the real number line, covering every possible magnitude.
  
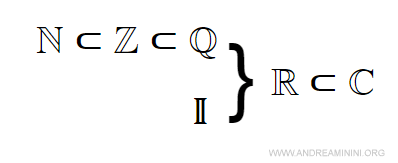
• Set of complex numbers (C)
  The set of complex numbers further extends the real numbers by including solutions to equations involving the square roots of negative numbers. Each complex number can be written in the form a + bi, where a and b are real numbers.