Real Numbers

What real numbers are

The set of real numbers is defined as the union of the rational numbers (Q) and the irrational numbers (I). It is conventionally denoted by the symbol R.

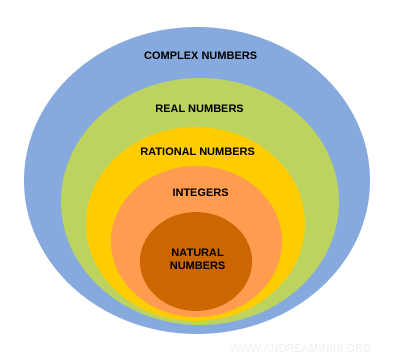
The real numbers comprise the sets of natural numbers, integers, rational numbers (for example 2/3), and irrational numbers (for example √2).

Note. The sets of rational numbers (Q) and irrational numbers (I) form a partition of the real numbers. A number is rational if it can be expressed as a ratio of two integers. A number is irrational if it cannot be expressed as such a ratio.

Operations on real numbers

For any pair of real numbers a,b, the following operations are defined

• Addition (+)
• Multiplication (·)
• Exponentiation (n^k)

together with their corresponding inverse operations

• Subtraction (-)
• Division (/)
• Root extraction (^k√n)

The following operations, however, are not defined within the real numbers

• Division by zero
• Even-index roots of negative numbers

Note. Even-index roots of negative numbers cannot be evaluated within the real numbers because no real number raised to an even power can yield a negative result. $$ \sqrt{-2} \ , \ \sqrt[4]{5} \ , \ \ldots $$ By contrast, odd-index roots of negative numbers are well defined in the real numbers. For example $$ \sqrt[3]{-8} = -2 \ \text{because} \ \ (-2) \cdot (-2) \cdot (-2) = -8 $$ To compute even-index roots of negative numbers, one must extend beyond the real numbers and introduce complex numbers, which constitute a numerical system strictly larger than the real numbers.

The set of real numbers is an infinite set, since it contains infinitely many elements.

The axioms of the real numbers

A] Axioms concerning addition and multiplication

1. Associative property $$ (a+b)+c = a+(b+c) $$ $$ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$

   Example. Let a=2, b=3, and c=4. The associative property for addition gives $$ (2+3)+4 = 2+(3+4) \\ 5+4 = 2+7 \\ 9 = 9 $$ and for multiplication $$ (2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4) \\ 6 \cdot 4 = 2 \cdot 12 \\ 24 = 24 $$

2. Commutative property $$ a+b = b+a $$ $$ a \cdot b = b \cdot a $$

   Example. Let a=2 and b=3. The commutative property for addition gives $$ 2+3 = 3+2 \\ 5 = 5 $$ and for multiplication $$ 2 \cdot 3 = 3 \cdot 2 \\ 6 = 6 $$

3. Distributive property $$ a \cdot (b+c) = a \cdot b + a \cdot c $$

Example. Let a=2, b=3, and c=4. $$ 2 \cdot (3+4) = 2 \cdot 3 + 2 \cdot 4 \\ 2 \cdot 7 = 6 + 8 \\ 14 = 14 $$

4. Identity elements
   Within the real numbers there exist two identity elements, one for addition and one for multiplication. $$ a+0 = a $$ $$ a \cdot 1 = a $$

   Example. $$ 5 + 0 = 5 $$ $$ 5 \cdot 1 = 5 $$

5. Additive inverses
   Every real number a admits an additive inverse -a such that their sum equals the additive identity $$ a+(-a) = 0 $$

   Example. $$ 5+(-5)=0 $$ $$ 7+(-7)=0 $$

6. Multiplicative inverses
   Every nonzero real number a admits a multiplicative inverse a^-1 such that their product equals the multiplicative identity, namely 1 $$ a \cdot a^{-1} = 1 $$

   Example. $$ 5 \cdot 5^{-1} = 5 \cdot \frac{1}{5} = 1 $$

B] Order axiom

Given any pair of real numbers a,b, the relation less than or equal to (≤) defines a total order, provided the following properties hold.

• For any two real numbers a,b, exactly one of the relations a≤b or a≥b holds. This is known as the dichotomy property.
• If both relations a≤b and a≥b hold for two real numbers a,b, then a=b. This is the antisymmetry property.
• If a≤b, then for any real number c the inequality a+c≤b+c also holds.
• If 0≤a and 0≤b, then both 0≤a+b and 0≤a*b hold.

C] The axiom of completeness

Given two nonempty sets A and B of real numbers such that a≤b for every a∈A and b∈B, there exists a real number c satisfying a≤c≤b. This statement is equivalent to the Dedekind completeness of the real numbers.

The difference between real, integer, natural, and rational numbers

The set of real numbers (R) contains several numerical subsets, each of which satisfies only a subset of the axioms characterizing the real numbers.

$$ N ⊆ Z ⊆ Q ⊆ R $$

These inclusions can be illustrated using Venn diagrams

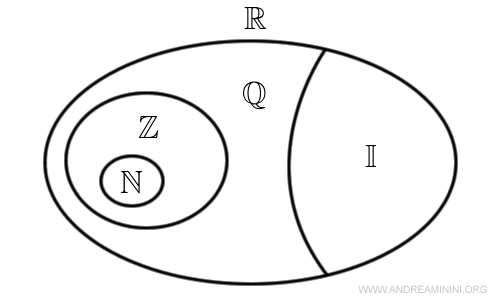
• Natural numbers (N). The set of natural numbers does not satisfy the axiom of additive inverses.

  Example. There is no natural number that is the additive inverse of 5, since -5 is not a natural number.

  Addition and multiplication are always defined, whereas the inverse operations of subtraction and division are not always possible.
• Integers (Z). The set of integers does not satisfy the axiom of multiplicative inverses. Only the integer 1 satisfies this property.

  Example. There is no integer that is the multiplicative inverse of 7, since 1/7, that is 7^-1, is not an integer.

  Within the integers, addition, multiplication, and subtraction are always defined. Division, however, cannot in general be performed between two integers.
• Rational numbers (Q). The set of rational numbers does not satisfy the axiom of completeness because it is not closed under the extraction of roots.

  Example. There is no rational number x=m/n such that x² = 2.

  Rational numbers allow addition, multiplication, subtraction, and division. Nevertheless, they fail to satisfy the completeness axiom with respect to the existence of all roots.

The set of real numbers is dense and complete

The set of real numbers is a dense and complete numerical set.

• It is dense because, given any two distinct real numbers a and b, there always exists another real number c such that a<c< b.
• It is complete because every nonempty subset of real numbers that is bounded above admits a least upper bound in R.

Consequently, the set of real numbers is in one-to-one correspondence with the set of points on the number line.

And so on.