Irrational Numbers
What irrational numbers are
The set of irrational numbers consists of all real numbers that cannot be expressed as the ratio of two integers.
Irrational numbers therefore have decimal expansions that are infinite and non-repeating.
Many irrational numbers arise from taking roots, such as √2, √3, √5, √7, and so on.
Others do not originate from roots. A well-known example is the constant pi, π = 3.14159..., defined as the ratio of a circle's circumference to its diameter.
Why they are called irrational
The term "irrational" is defined by contrast with rational numbers.
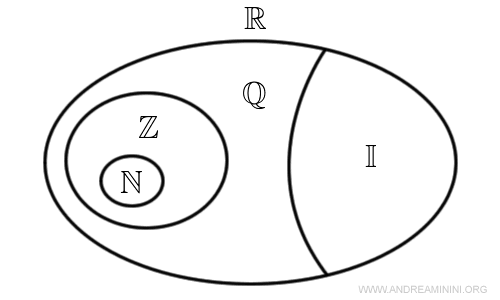
What are rational numbers? A real number (R) is said to be rational (Q) if it can be written as the ratio of two integers. For example, the real number 2.5 is rational because it can be expressed as 5/2. However, not all real numbers can be obtained as the ratio of two integers.
All real numbers that are not rational are called irrational (I).
A concrete example
The square root of 3 is a real number.
$$ \sqrt{3} = 1.73205080757 \in R $$
However, it cannot be expressed as the ratio of two integers.
No pair of integers m and n satisfies the equation whose solution is the square root of 3.
$$ \frac{m}{n} = \sqrt{3} $$
Therefore, √3 is not a rational number.
$$ \sqrt{3} \notin Q $$
The square root of 3 is an irrational number.
$$ \sqrt{3} \in I $$
Note. The same reasoning applies to other roots that cannot be expressed exactly using square roots, cube roots, or higher-order roots. $$ \sqrt{7} \\ \sqrt[3]{5} \\ \sqrt[4]{6} \\ \vdots $$ However, this argument does not apply to all roots, because some roots belong to the set of rational numbers. For example $$ \sqrt{9} = 3 = \frac{6}{2} $$ Moreover, some roots do not belong to the set of real numbers at all. In such cases, they are neither rational nor irrational. For instance, there is no real number whose square equals -1. $$ \sqrt{-1} \notin R $$ This last root belongs to the set of complex numbers.
How to determine whether a number is irrational
To determine whether a number is irrational, one can use the method of successive approximations.
For example, let us determine whether the square root of 2 is irrational.
$$ \sqrt{2}$$
First, we identify two integers whose squares bound √2 from below and from above.
$$ 1 < \sqrt{2} < 2 $$
Note. To find these two integers, square all terms of the inequality. $$ x \le \sqrt{2} \le y $$ $$ x^2 \le ( \sqrt{2} )^2 \le y^2 $$ $$ x^2 \le 2 \le y^2 $$ We then look for two integers x and y that bound 2 as tightly as possible from below and from above. In this case, x = 1 and y = 2. $$ 1^2 \le 2 \le 2^2 $$
As a second approximation, we look for two decimal numbers with one decimal place that bound √2 more accurately.
$$ 1.4 < \sqrt{2} < 1.5 $$
Note. To find these values, we start from the previous lower bound (1) and progressively add decimal digits until the square exceeds 2. $$ 1.0^2 = 1 \\ 1.1^2 = 1.21 \\ 1.2^2 = 1.44 \\ 1.3^2 = 1.69 \\ 1.4^2 = \color{green}{1.96 } \\ 1.5^2 = \color{red}{2.25} $$ The best one-decimal approximation from below is 1.4, while the best approximation from above is 1.5.
As a third approximation, we repeat the same procedure to find two numbers with two decimal places.
$$ 1.41 < \sqrt{2} < 1.42 $$
Note. The procedure for identifying the two bounds is always the same. In this case, the previous lower bound is 1.4. $$ 1.40^2 = 1.96 \\ 1.41^2 = \color{green}{1.9881} \\ 1.42^2 = \color{red}{2.0164} $$ The best two-decimal approximation from below is 1.41, while the best approximation from above is 1.42.
As a fourth approximation, we look for two numbers with three decimal places.
$$ 1.414 < \sqrt{2} < 1.415 $$
Note. We repeat the same search procedure. In this case, the previous lower bound is 1.41. $$ 1.410^2 = 1.9881 \\ 1.411^2 = 1.990921 \\ 1.412^2 = 1.993744 \\ 1.413^2 = 1.996569 \\ 1.414^2 = \color{green}{1.999396} \\ 1.415^2 = \color{red}{2.002225} $$ The best approximation from below is 1.414, while the best approximation from above is 1.415.
As a fifth approximation, we look for two numbers with four decimal places.
$$ 1.4142 < \sqrt{2} < 1.4143 $$
As a sixth approximation, we look for two numbers with five decimal places.
$$ 1.41421 < \sqrt{2} < 1.41422 $$
As a seventh approximation, we look for two numbers with six decimal places.
$$ 1.414213 < \sqrt{2} < 1.414214 $$
As an eighth approximation, we look for two numbers with seven decimal places.
$$ 1.4142135 < \sqrt{2} < 1.4142136 $$
At this point, two observations can already be made.
- The lower and upper bounds converge progressively but never coincide. This shows that the square root of 2 is not a terminating decimal. It is an infinite decimal.
- The decimal expansion is infinite and exhibits no repeating pattern. Therefore, the square root of 2 is not periodic. It is a non-repeating decimal.
In conclusion, the square root of 2 is neither a terminating decimal nor a repeating infinite decimal.
Therefore, √2 does not belong to the set of rational numbers.
Consequently, the square root √2 is an irrational number, that is, a non-rational real number.
And so on.
